Những hằng đẳng thức xứng đáng nhớ kiên cố rất gần gũi gì với chúng ta . Hôm ni Kiến tiếp tục thưa kỹ rộng lớn về 7 hằng đẳng thức cần thiết : bình phương của một tổng, bình phương của một hiệu, hiệu của nhì bình phương, lập phương của một tổng, lập phương của một hiệu, tổng nhì lập phương và sau cùng là hiệu nhì lập phương. Các chúng ta nằm trong tìm hiểu thêm nhé. Bạn đang xem: a bình cộng b bình
1. Bình phương của một tổng
Với A, B là những biểu thức tùy ý, tớ có: ( A + B )2 = A2 + 2AB + B2.
Ví dụ:
a) Tính ( a + 3 )2.b) Viết biểu thức x2+ 4x + 4 bên dưới dạng bình phương của một tổng.
Hướng dẫn:
a) Ta có: ( a + 3 )2= a2+ 2.a.3 + 32 = a2 + 6a + 9.
b) Ta đem x2+ 4x + 4 = x2+ 2.x.2 + 22 = ( x + 2 )2.
2. Bình phương của một hiệu
Với A, B là những biểu thức tùy ý, tớ có: ( A - B )2 = A2 - 2AB + B2.
3. Hiệu nhì bình phương
Với A, B là những biểu thức tùy ý, tớ có: A2 - B2 = ( A - B )( A + B ).
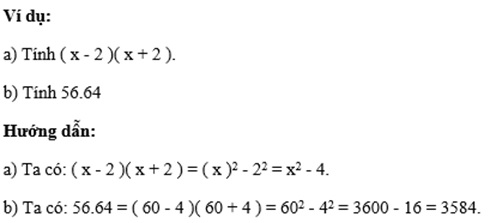
4. Lập phương của một tổng
Với A, B là những biểu thức tùy ý, tớ có: ( A + B )3 = A3 + 3A2B + 3AB2 + B3.
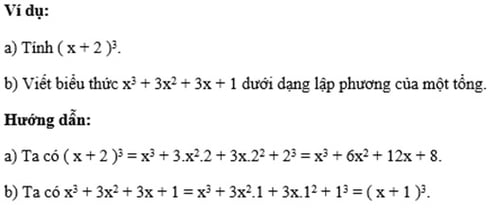
5. Lập phương của một hiệu.
Với A, B là những biểu thức tùy ý, tớ có: ( A - B )3 = A3 - 3A2B + 3AB2 - B3.
Ví dụ :
a) Tính ( 2x - 1 )3.b) Viết biểu thức x3- 3x2y + 3xy2- y3 dưới dạng lập phương của một hiệu.
Hướng dẫn:
a) Ta có: ( 2x - 1 )3= ( 2x )3 - 3.( 2x )2.1 + 3( 2x ).12 - 13
= 8x3 - 12x2 + 6x - 1
b) Ta đem : x3- 3x2y + 3xy2- y3= ( x )3 - 3.x2.hắn + 3.x. y2 - y3
= ( x - hắn )3
6. Tổng nhì lập phương
Với A, B là những biểu thức tùy ý, tớ có: A3 + B3 = ( A + B )( A2 - AB + B2 ).
Chú ý: Ta quy ước A2 - AB + B2 là bình phương thiếu hụt của hiệu A - B.
Ví dụ:
a) Tính 33+ 43.b) Viết biểu thức ( x + 1 )( x2- x + 1 ) bên dưới dạng tổng nhì lập phương.
Hướng dẫn:
a) Ta có: 33+ 43= ( 3 + 4 )( 32 - 3.4 + 42 ) = 7.13 = 91.
b) Ta có: ( x + 1 )( x2- x + 1 ) = x3+ 13 = x3 + 1.
Xem thêm: Tường Thuật Trực Tiếp Bóng Đá Hôm Nay Trên 90P TV
7. Hiệu nhì lập phương
Với A, B là những biểu thức tùy ý, tớ có: A3 - B3 = ( A - B )( A2 + AB + B2 ).
Chú ý: Ta quy ước A2 + AB + B2 là bình phương thiếu hụt của tổng A + B.
Ví dụ:
a) Tính 63- 43.b) Viết biểu thức ( x - 2y )( x2+ 2xy + 4y2) bên dưới dạng hiệu nhì lập phương
Hướng dẫn:
a) Ta có: 63- 43= ( 6 - 4 )( 62 + 6.4 + 42 ) = 2.76 = 152.b) Ta đem : ( x - 2y )( x2+ 2xy + 4y2) = ( x )3 - ( 2y )3 = x3 - 8y3.
B. Bài tập dượt tự động luyện về hằng đẳng thức
Bài 1.Tìm x biết
a) ( x - 3 )( x2+ 3x + 9 ) + x( x + 2 )( 2 - x ) = 0.b) ( x + 1 )3- ( x - 1 )3- 6( x - 1 )2 = - 10.
Hướng dẫn:
a) sát dụng những hằng đẳng thức ( a - b )( a2+ ab + b2) = a3 - b3.( a - b )( a + b ) = a2 - b2.
Khi ê tớ đem ( x - 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 - x ) = 0.
⇔ x3 - 33 + x( 22 - x2 ) = 0 ⇔ x3 - 27 + x( 4 - x2 ) = 0
⇔ x3 - x3 + 4x - 27 = 0
⇔ 4x - 27 = 0
Vậy x= 
( a + b )3 = a3 + 3a2b + 3ab2 + b3
( a - b )2 = a2 - 2ab + b2
Khi ê tớ có: ( x + 1 )3 - ( x - 1 )3 - 6( x - 1 )2 = - 10.
⇔ ( x3 + 3x2 + 3x + 1 ) - ( x3 - 3x2 + 3x - 1 ) - 6( x2 - 2x + 1 ) = - 10
⇔ 6x2 + 2 - 6x2 + 12x - 6 = - 10
⇔ 12x = - 6
Vậy x=
Bài 2: Rút gọn gàng biểu thức A = (x + 2y ).(x - 2y) - (x – 2y)2
- 2x2+ 4xy B. – 8y2+ 4xy
- - 8y2 D. – 6y2+ 2xy
Hướng dẫn
Ta có: A = (x + 2y ). (x - 2y) - (x – 2y)2
A = x2 – (2y)2 – [x2 – 2.x.2y +(2y)2 ]
A = x2 – 4y2 – x2 + 4xy - 4y22
Xem thêm: văn tả con chó lớp 4 ngắn gọn nhất
A = -8y2 + 4xy
- Hãy lưu giữ nó nhé
Những hằng đẳng thức xứng đáng nhớ bên trên đặc biệt cần thiết tủ kỹ năng và kiến thức của tất cả chúng ta . Thế nên chúng ta hãy phân tích và ghi lưu giữ nó nhé. Những đẳng thức ê chung tất cả chúng ta xử lý những Việc dễ dàng và khó khăn một cơ hội đơn giản và dễ dàng, chúng ta nên thực hiện đi làm việc lại nhằm phiên bản thân thiện rất có thể áp dụng đảm bảo chất lượng rộng lớn. Chúc chúng ta thành công xuất sắc và chuyên cần bên trên tuyến đường học hành. Hẹn chúng ta ở những bài bác tiếp theo
Bình luận