Giúp chúng ta học viên mò mẫm hiểu về những tình huống đều nhau của tam giác vuông nhằm hoàn toàn có thể giải những vấn đề về tam giác vuông thiệt nhanh gọn lẹ.
Các tình huống đều nhau của tam giác vuông là tổ hợp những kỹ năng kể từ định nghĩa về tam giác đều nhau và những tình huống nhì tam giác vuông đều nhau. Với những kỹ năng này sẽ hỗ trợ chúng ta học viên đạt được hành trang vững vàng vàng nhằm hoàn thiện thiệt chất lượng tốt những bài xích luyện hình học tập về tam giác đều nhau và tam giác vuông.
Bạn đang xem: cạnh huyền cạnh góc vuông
1. Hai tam giác đều nhau là gì?
Hai tam giác được gọi là đều nhau Lúc nhưng mà nhì tam giác bại liệt sở hữu những cạnh ứng đều nhau và những góc ứng cũng đều nhau.
Để kí hiệu sự đều nhau của tam giác ABC và tam giác DFE.
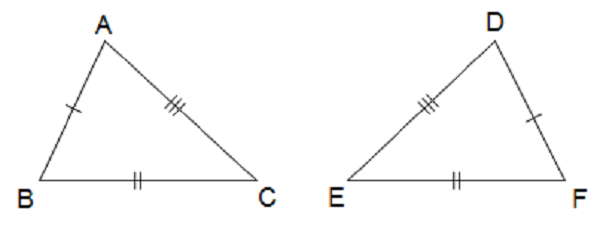
Hai tam giác vì thế nhau
2. Các tình huống đều nhau của tam giác vuông
Tam giác vuông là 1 trong tam giác khá đặc trưng vì thế có một góc vuông. Vì thế nhưng mà Lúc đối chiếu nhì tam giác vuông thì chỉ việc 2 tam giác bại liệt được thêm 2 điểm cộng đồng nữa thì nó được gọi là đều nhau. Sau phía trên, công ty chúng tôi tiếp tục trình làng với những bạn những tình huống đều nhau của tam giác vuông.
2.1 Hai cạnh góc vuông
Hai tam giác vuông được gọi là đều nhau nếu như nhì cạnh ngay lập tức kề góc vuông của tam giác này theo thứ tự vì thế nhì cạnh ngay lập tức kề góc vuông của tam giác vuông bại liệt. (cạnh – góc – cạnh )
2.2 Cạnh góc vuông và góc nhọn ngay lập tức kề cạnh đó
Hai tam giác vuông được gọi là đều nhau nếu như một cạnh góc vuông và một góc nhọn kề kề bên ấy của tam giác vuông này vì thế một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông bại liệt. ( góc – cạnh – góc )
2.3 Cạnh huyền, góc nhọn
Hai tam giác vuông được gọi là đều nhau nếu như một góc nhọn và cạnh huyền của tam giác vuông này vì thế một góc nhọn và cạnh huyền của tam giác vuông bại liệt. ( góc – cạnh – góc)
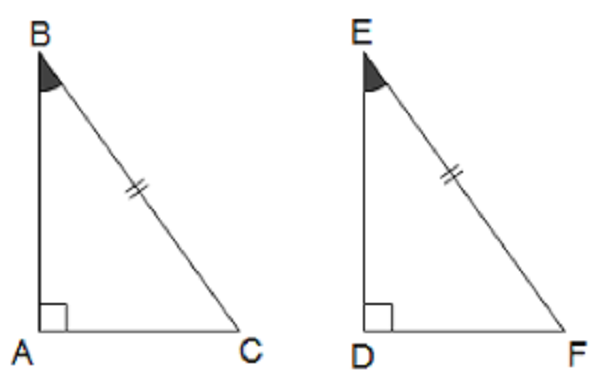
Hai tam giác vuông đều nhau theo gót cạnh huyền và góc nhọn
2.4 Cạnh huyền và cạnh góc vuông
Hai tam giác vuông được gọi là đều nhau nếu như một cạnh của góc vuông và cạnh huyền của tam giác vuông này vì thế một cạnh của góc vuông và cạnh huyền của tam giác vuông bại liệt.
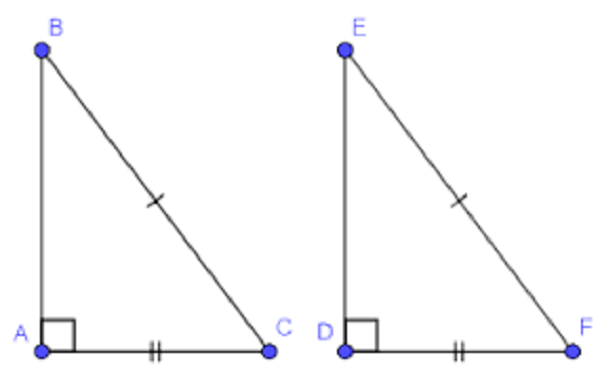
Hai tam giác vuông đều nhau theo gót cạnh huyền và cạnh góc vuông
3. Các dạng bài xích về những tình huống đều nhau của tam giác vuông
Ở bên trên, công ty chúng tôi tiếp tục trình làng về các tình huống đều nhau của tam giác vuông. Tuy nhiên, nhằm những em học viên hoàn toàn có thể hiểu và nắm vững rộng lớn về những định nghĩa này tất cả chúng ta tiếp tục nằm trong mò mẫm hiểu qua chuyện những ví dụ sau đây:
Dạng 1: Chứng minh những tam giác vuông vì thế nhau
Ở dạng này tất cả chúng ta tiếp tục xét nhì tam giác vuông, rồi đánh giá những ĐK vì thế nhau: cạnh - góc - cạnh, góc - cạnh - góc, cạnh huyền - góc nhọn hoặc cạnh huyền - cạnh góc vuông. Từ bại liệt, xác lập coi nhì tam giác bại liệt đều nhau theo gót tình huống nào là và thể hiện tóm lại nhì tam giác đều nhau.
Dạng 2: Chứng minh góc và đoạn trực tiếp vì thế nhau
Với dạng bài xích này cũng tiếp tục áp dụng những kỹ năng về những tình huống đều nhau của nhì tam giác vuông. Từ bại liệt, minh chứng nhì tam giác đều nhau thì những đoạn trực tiếp và những góc cũng đều nhau.
Nếu các bạn thấy tam giác vuông thì nên cần mò mẫm tăng nhì ĐK đều nhau, vô bại liệt sở hữu tối thiểu một ĐK về cạnh nhằm minh chứng nhì tam giác này là đều nhau vậy mới nhất hoàn toàn có thể minh chứng nhì cạnh hoặc góc ứng đều nhau.
Dạng 3: Tìm tăng những ĐK nhằm nhì tam giác vuông đều nhau.
Với dạng bài xích này trước tiên bạn phải gọi kĩ đề bài xích và vẽ hình nhằm hoàn toàn có thể coi nhì tam giác vuông tiếp tục sở hữu những nguyên tố nào là đều nhau. Từ bại liệt, các bạn đo lường và tính toán tăng coi rất cần phải bổ sung cập nhật tăng ĐK nào là nhằm nhì tam giác vuông bại liệt hoàn toàn có thể vì thế nhau
4. Giải một vài ví dụ minh họa những tình huống đều nhau của tam giác
Ví dụ 1:
Cho tam giác MNP cân nặng bên trên M. Kẻ MH vuông góc với NP. Chứng minh :
a) HN = HP
b) góc NMH = góc PMH
Trả lời:
a) Xét nhì tam giác vuông ΔMNH và ΔMPH tao có: MN = MP theo gót fake thiết và AH là cạnh cộng đồng. Suy ra: ΔMNH = ΔMPH theo gót tình huống cạnh huyền - cạnh góc vuông.
Suy ra: HN = HP (cặp cạnh tương ứng)
b) Ta có: Hai tam giác ΔMNH = ΔMPH (chứng minh trên). Vậy nên sẽ sở hữu được góc NMH = góc PMH
Ví dụ 2:
Xem thêm: ngày xuân con én đưa thoi
Các tam giác vuông ABC và MNP sở hữu góc A và góc M đều nhau và vì thế 90 phỏng, AC = MP. Hãy thêm 1 ĐK nhằm nhì tam giác ΔABC = ΔMNP.
Bài giải:
Nếu tăng AB =MN thì tao sẽ sở hữu được nhì tam giác ΔABC = ΔMNP theo gót tình huống cạnh - góc - cạnh.
Nếu tăng góc C = góc P.. thì tao sẽ sở hữu được nhì tam giác ΔABC và ΔMNP đều nhau theo gót tình huống góc - cạnh – góc.
Còn Lúc tăng BC = NP thì tao sẽ sở hữu được ΔABC = ΔMNP theo gót tình huống cạnh huyền - cạnh góc vuông.
Ví dụ 3:
Cho tam giác DEF cân nặng bên trên điểm D, góc D nhỏ rộng lớn 90o. Vẽ EK ⊥ DF (K ∈ DF), CH ⊥ DE (H ∈ DE).
a) Chứng minh rằng DK = KH
b) Gọi M là giao phó điểm của EK và CH. Chứng minh rằng đoạn trực tiếp DM đó là tia phân giác của góc D
Bài giải
a) Giả thiết ΔDEF cân nặng bên trên D thì sở hữu DE = DF. Xét nhì tam giác vuông KDE và HDF, tao có:
DE = DF (chứng minh trên), góc D cộng đồng.
⇒ ΔKDE = ΔHDF theo gót (cạnh huyền - góc nhọn)
⇒ DK = DH (cặp cạnh tương ứng)
b) Xét nhì tam giác vuông HDM và KDM, tao có:
DK = DH (chứng minh trên), DM là cạnh cộng đồng của nhì tam giác. Từ bại liệt, suy rời khỏi ΔKDM = ΔHDM (cạnh huyền - cạnh góc vuông) và cặp góc ứng là góc KDM = góc HDM. Vậy tia DM đó là tia phân giác của góc D.
5. Tổng hợp ý những dạng bài xích luyện tam giác vuông vì thế nhau
Dưới đó là tổ hợp những dạng bài xích luyện lý thuyết và thực hành thực tế về các tình huống đều nhau của tam giác vuông.
5.1 Bài luyện lý thuyết
Bài 1: Hãy nêu các tình huống đều nhau của tam giác vuông? Vẽ hình hình ảnh minh họa mang lại từng ngôi trường hợp?
Bài 2: Phát biểu toan lí hai tuyến phố trực tiếp nằm trong vuông góc với cùng 1 lối thẳng? Nêu fake thiết, kết luận? Vẽ hình minh họa.
Bài 3: Nêu định nghĩa nhì tam giác vì thế nhau? Vẽ hình minh?
5.2 Bài luyện thực hành
Bài 1: Cho tam giác ABC và tam giác DEF biết góc A = góc D = 90°, góc C = góc F. Cần bổ sung cập nhật tăng ĐK gì nhằm nhì tam giác ABC và tam giác DEF đều nhau theo gót tình huống cạnh góc vuông – góc nhọn kề?
A. AC = DF B. AB = DE C. BC = EF D. AC = DE
Bài 2: Cho tam giác ABC và tam giác DEF sở hữu góc B và góc E đều nhau và vì thế 90°, AC = DF, góc A = góc F. Hãy mò mẫm tuyên bố đích thị trong mỗi tuyên bố sau đây?
A. ΔABC = ΔFED B. ΔABC = ΔFDE C. ΔBAC = ΔFED D. ΔABC = ΔDEF
Bài 3: Cho tam giác ABC, kẻ BE và CD theo thứ tự là lối cao vuông góc với những cạnh AC, AB. Chứng minh rằng nhì tam giác BCD và CBE đều nhau, biết BD = EC.
Bài 4: Cho tam giác ACD cân nặng bên trên A. Từ đỉnh A kẻ AH vuông góc với CD, H thuộc CD. Chứng minh rằng: HB = HC và AH là tia phân giác của góc BAC.
Xem thêm: chuỗi truyền electron tạo ra
Bài 5: Cho nhì tam giác ABC và DEF theo thứ tự vuông bên trên A và D, biết AB = DE. a) Để nhì tam giác bên trên hoàn toàn có thể đều nhau theo gót tình huống cạnh góc vuông và góc nhọn kề thì nên cần tăng ĐK gì?
b) Để nhì tam giác bên trên hoàn toàn có thể đều nhau theo gót tình huống cạnh huyền và góc nhọn kề thì nên cần tăng ĐK gì?
Trên phía trên, công ty chúng tôi tiếp tục tổ hợp và cung ứng cho tới chúng ta những thông tin cẩn tương quan đến các tình huống đều nhau của tam giác vuông và một vài bài xích luyện nhưng mà chúng ta có thể áp dụng. Mong rằng với những gì công ty chúng tôi cung ứng sẽ hỗ trợ việc học tập và thực hiện những bài xích luyện toán của chúng ta nhỏ trở lên trên đơn giản rộng lớn.











Bình luận