Toán 12 | Cách làm bài cực trị hàm trị tuyệt đối nhanh

Cực trị hàm trị tuyệt đối chính là dạng bài xích kha khá dễ dàng nằm trong chuyên nghiệp đề Cực trị hàm số trong lịch trình Toán 12. butbi van share cho tới chúng ta phương pháp để thực hiện nhanh chóng bài xích xác lập vô cùng trị của hàm trị vô cùng nhanh chóng – gọn gàng – đúng đắn. Hãy nằm trong thăm dò hiểu

GIẢI PHÁP HỌC TỐT 12

Bạn đang xem: cực trị hàm trị tuyệt đối

XUẤT PHÁT SỚM ĐỖ ĐẠI HỌC SỚM

✅ Lộ trình chuẩn chỉnh 4 bước: Học – Luyện – Hỏi – Kiểm Tra

✅ Cung cung cấp khối hệ thống bài xích giảng, đề chính, phủ đầy đủ kỹ năng THPT

✅ Trang bị cách thức, phương án thực hiện bài xích tự động luận, trắc nghiệm

✅ Kho bài xích tập dượt, đề đánh giá to con ở từng học tập lực

✅ Đội ngũ nghề giáo phổ biến, nhiều kinh nghiệm

Tham khảo thêm:

Cực trị của hàm số
Các dạng toán về vô cùng trị với thông số so với những hàm số đơn giản

a) Hàm trị vô cùng là gì?

Hàm trị vô cùng tương tự như tên thường gọi, nó đó là những hàm số với chứa chấp trị vô cùng. Hàm trị tuyệt cồn thường thì sẽ có được 2 dạng là:

Y = |f(x)|
Y = f(|x|)

b) Cách thực hiện bài xích cực trị hàm trị tuyệt đối nhanh

– Phương pháp thực hiện bài xích vô cùng trị của hàm trị tuyệt so với hàm số nó = |f(x)|

Để hoàn toàn có thể tìm kiếm được vô cùng trị của hàm số với dạng: nó = |f(x)|, việc trước tiên tất cả chúng ta cần thiết thực hiện là lập bảng bảng thiên và tổ chức vẽ đồ gia dụng thị hàm số nó = |f(x)|.

Để hoàn toàn có thể vẽ được đồ gia dụng thị của hàm nó = |f(x)|, tao hoàn toàn có thể dựa vào đồ gia dụng thị hoặc bảng vươn lên là thiên của hàm số nó = f(x) .

Lưu ý cho những bạn:

Đối với đồ gia dụng thị của hàm số nó = |f(x)| tiếp tục bao hàm 2 phần:

Phần đồ gia dụng thị hàm số nó = f(x) phía trên trục hoành (trục OX nhé)
Phần đồ gia dụng thị lấy đối xứng với nó = f(x) tiếp tục ở bên dưới trục OX qua quýt trục Ox của đồ gia dụng thị

– Phương pháp thực hiện bài xích vô cùng trị của hàm trị tuyệt so với hàm số nó = f(|x|)

Để thăm dò vô cùng trị của hàm trị tuyệt khái niệm dạng nó = f(|x|) tao cần được lập bảng thiên hoặc vẽ đồ gia dụng thị của hàm số nó = f(|x|) trải qua việc xác lập của bảng vươn lên là thiên hoặc đồ gia dụng thị của hàm số nó = f(x) .

Lưu ý cho những bạn:

Đồ thị hàm số trị tuyệt khái niệm dạng nó = f(|x|) tiếp tục bao hàm 2 phần chính:

Phần đồ gia dụng thị với dạng nó = f(x) nó nằm cạnh sát nên trục tung (trục OY nhé) (gọi đó là C)
Phần đồ gia dụng thị lấy đối xứng (C) trải qua qua quýt OY

2. Số vô cùng trị của hàm trị vô cùng – Lý thuyết

a) Số vô cùng trị của hàm trị tuyệt so với hàm số nó = |f(x)|

Số điểm vô cùng trị của hàm số trị tuyệt khái niệm dạng nó = |f(x)| tiếp tục vì chưng tổng số điểm vô cùng trị của hàm số nó = f(x) nằm trong vớii số nghiệm bội lẻ của phương trình với dạng [y=f(x)] = 0

b) Số vô cùng trị của hàm trị tuyệt so với hàm số nó = f(|x|)

Số điểm vô cùng trị của hàm trị vô cùng so với hàm số với dạng nó = f(|x|) tiếp tục gấp hai số điểm vô cùng trị dương của hàm số nó = f(x) thêm vào đó với một.

3. Các dạng bài xích cực trị hàm trị tuyệt đối tham lam khảo

*Ví dụ 1: Cho hàm số nó = f(x) với đồ gia dụng thị (C) như hình vẽ bên dưới. Hãy xác lập hàm trị vô cùng nó = f(|x|) bao gồm với từng nào điểm vô cùng trị?

A. 3

B. 2

C. 5

D. 7

Lời giải chi tiết:

Đáp án đúng: C (5 điểm vô cùng trị)

Đồ thị (C’) của hàm số nó = f(|x|) sẽ có được dạng như sau:

Giữ nguyên vẹn phần đồ gia dụng thị ở phía ở bên phải trục tung của(C) tao được (C₁)
Tiến hành vẽ đối xứng qua quýt trục tung phần đồ gia dụng thị của (C₁) tao sẽ tiến hành đồ gia dụng thị (C₂)
Khi cơ đồ gia dụng thị của hàm nó = f(|x|) đó là kí thác của (C₁)(C₂). Đồ thị sẽ có được dạng như hình vẽ bên dưới đây:

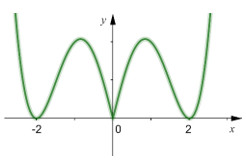
Từ đồ gia dụng thị (C’) tao hoàn toàn có thể rút rời khỏi được Tóm lại hàm nó = f(|x|) sẽ có được tổng số 5 điểm vô cùng trị.

Hoặc tao hoàn toàn có thể vận dụng cơ hội giải nhanh chóng như sau: Nhìn vô đồ gia dụng thị (C) tao hoàn toàn có thể thấy được rằng đồ gia dụng thị với 2 điểm vô cùng trị dương ⇒ Số điểm vô cùng trị của hàm số nó = f(|x|) = 2×2+1 = 5.

*Ví dụ 2: Cho hàm số với dạng như sau: nó = f(x) với bảng vươn lên là thiên như hình bên dưới. Hãy xác lập hàm số nó = |f(x)| bao gồm với tổng số từng nào điểm vô cùng trị?

A. 5.

B. 4.

C. 2.

D. 7.

Xem thêm: hôm nay là thứ bảy

Lời giải chi tiết:

Đáp án đúng: D (7 điểm vô cùng trị)

Ta với đồ gia dụng thị hàm nó = |f(x)| tiếp tục bao gồm 2 phần.

Phần đồ gia dụng thị nó = f(x) tiếp tục nằm tại vị trí bên trên trục Ox
Phần đồ gia dụng thị lấy đối xứng nhìn qua quýt Ox của đồ gia dụng thị nó = f(x) tiếp tục nằm tại vị trí phía bên dưới trục Ox.

Đồ thị của hàm số nó = f(x) kí thác với trục Ox ở 4 điểm với hoành phỏng theo thứ tự này đó là x₁; x₂; x₃; x_4.

Vậy tao sẽ có được bảng vươn lên là thiên của đồ gia dụng thị nó = |f(x)| cụ thể như sau:

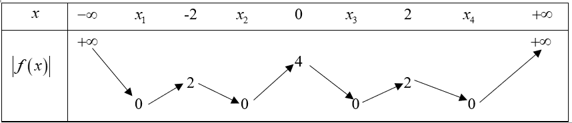
Thông qua quýt bảng vươn lên là thiên tao hoàn toàn có thể suy rời khỏi được đồ gia dụng thị nó = |f(x)| với tổng số 7 điểm vô cùng trị.

*Ví dụ 3: Cho hàm số với dạng nó = |(x – 1)(x – 2)²|. Xác quyết định tổng số điểm vô cùng trị của hàm trên?

A. 1.

B. 5.

C. 3.

D. 8.

Lời giải chi tiết:

Đáp án chủ yếu xác: C (3 điểm vô cùng trị)

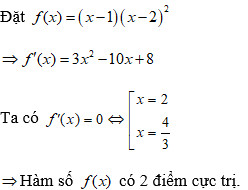
Bên cạnh cơ tao nhận thấy: f(x) = (x – 1)(x – 2)² = 0 có một nghiệm đơn này đó là x = 1

Ta có: số điểm vô cùng trị của hàm trị vô cùng nó = |(x – 1)(x – 2)²| đó là số điểm vô cùng trị của hàm số f(x) = (x – 1)(x – 2)² cộng với số nghiệm bội lẻ của phương trình f(x) = 0.

Như vậy tổng số điểm vô cùng trị của hàm số nó = |(x – 1)(x – 2)²| = 2 + 1 = 3 (điểm vô cùng trị)

4. Bài tập dượt cực trị hàm trị tuyệt đối với đáp án

*Ví dụ 1:

*Ví dụ 2:

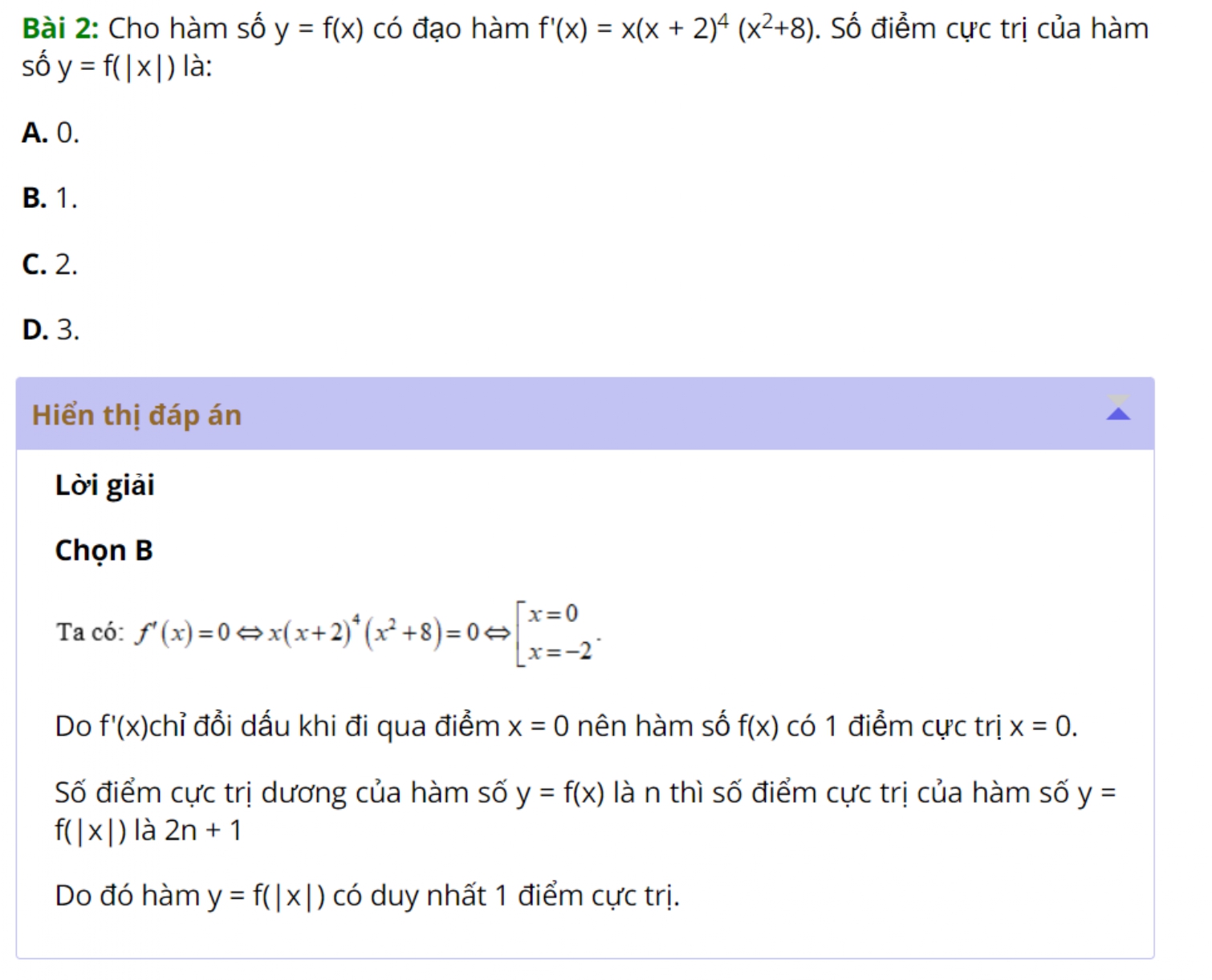
*Ví dụ 3:

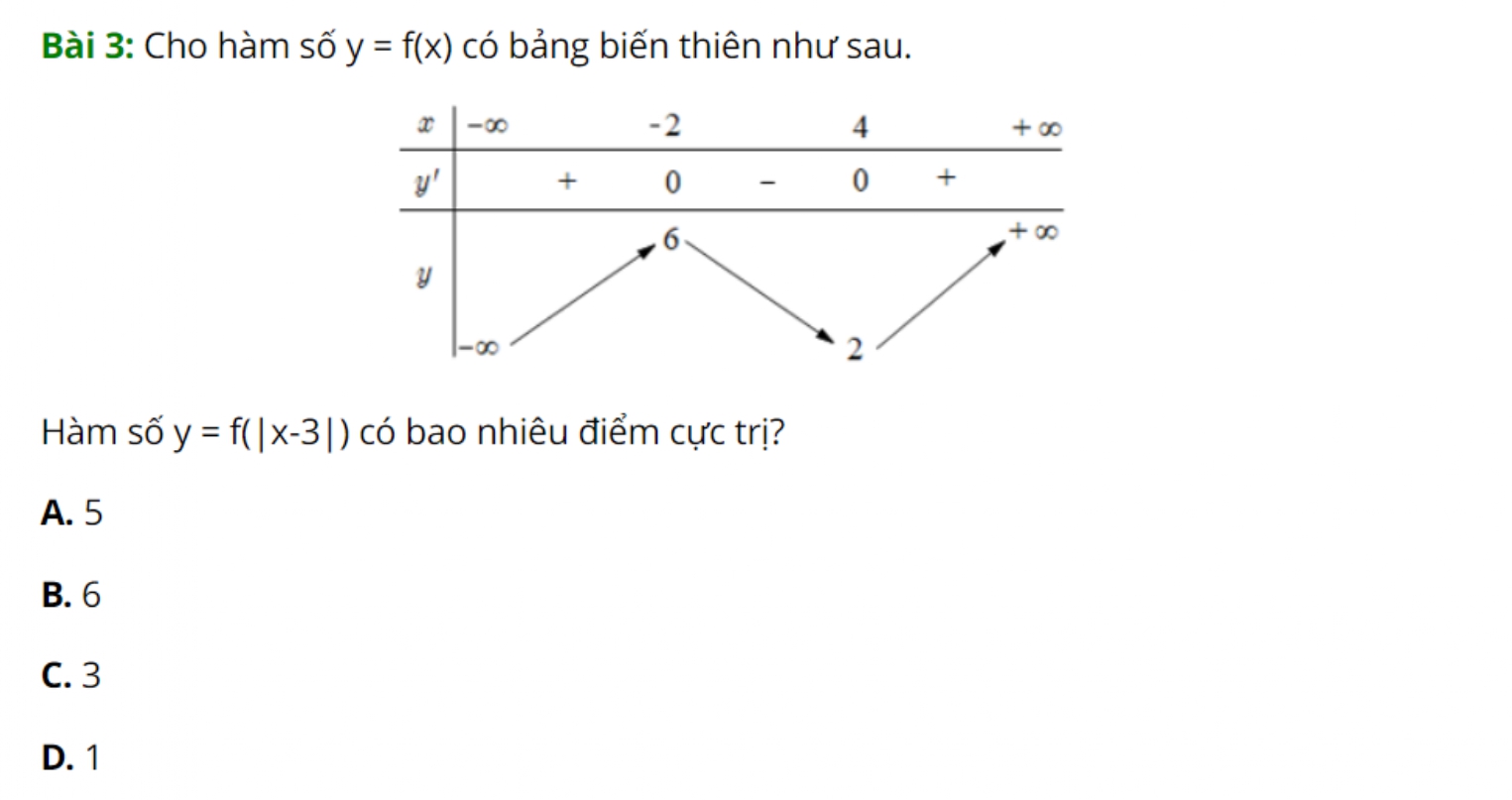
*Ví dụ 4:

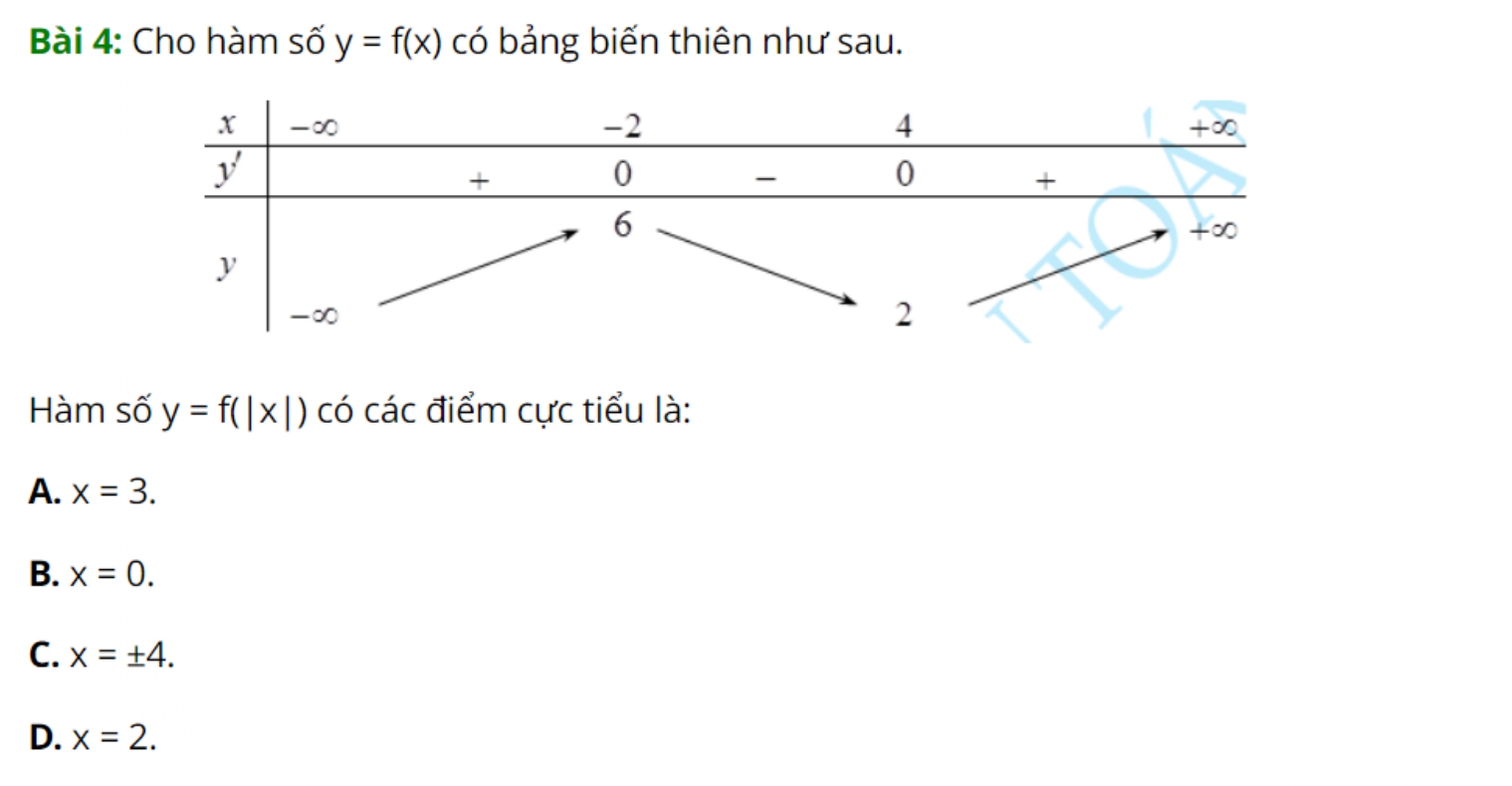
*Ví dụ 5:

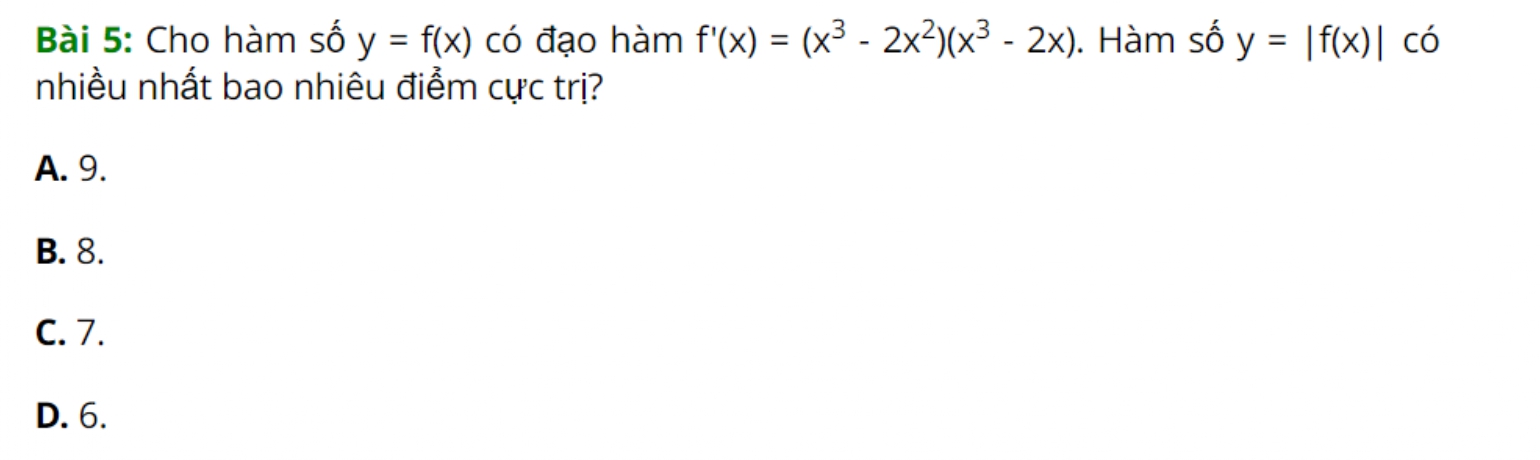
*Ví dụ 6:

*Ví dụ 7:

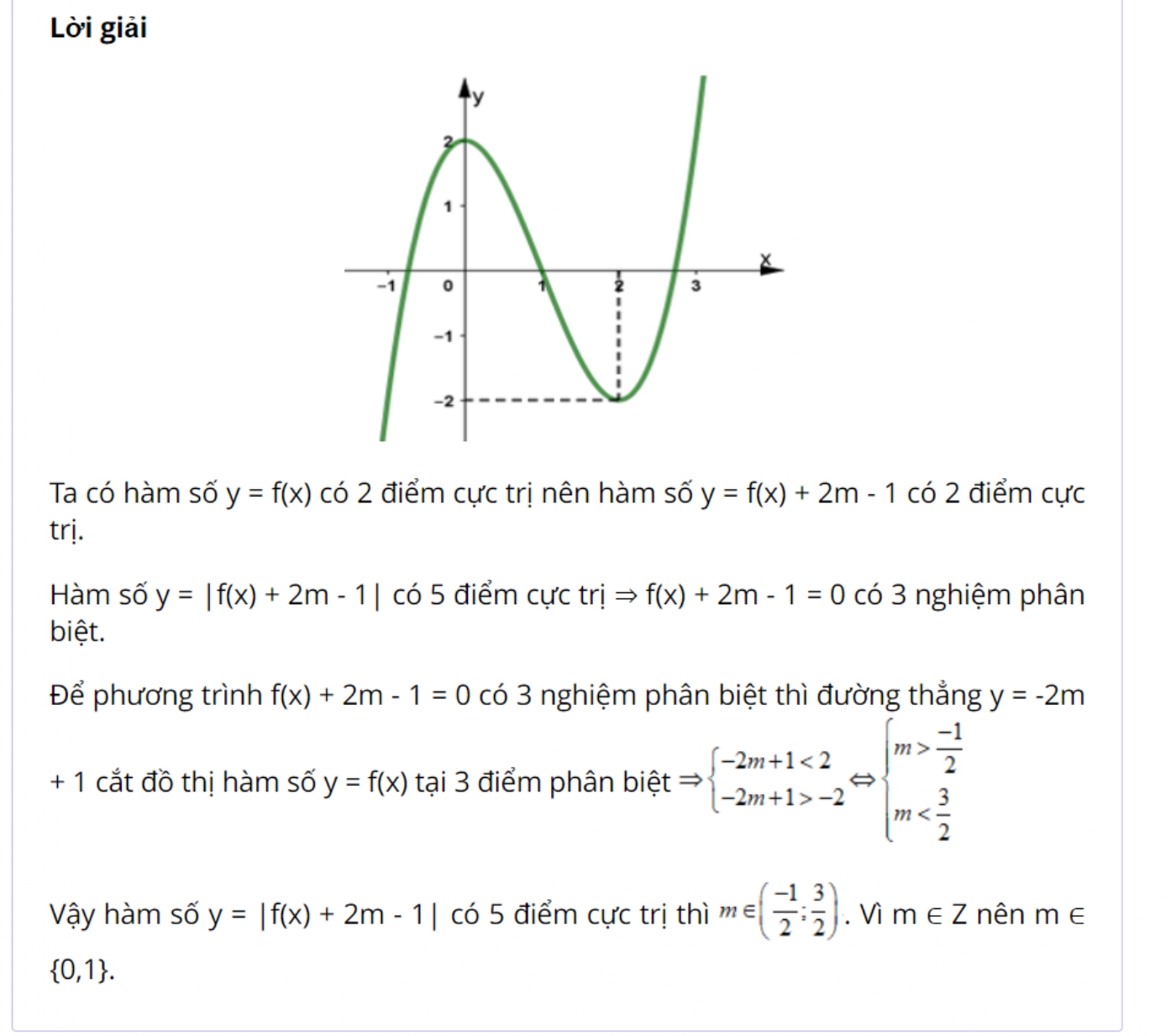
*Ví dụ 8:

*Ví dụ 9:

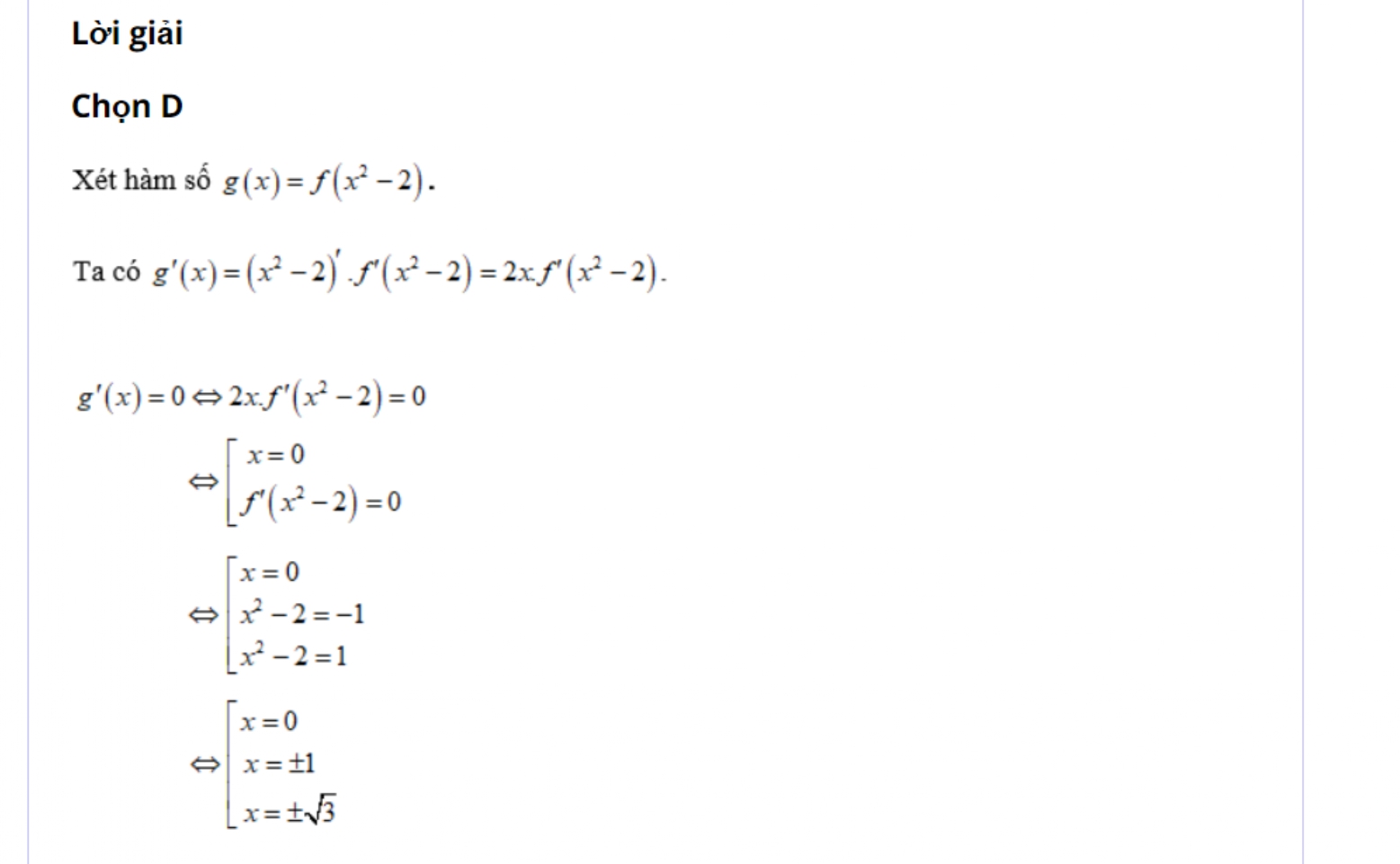
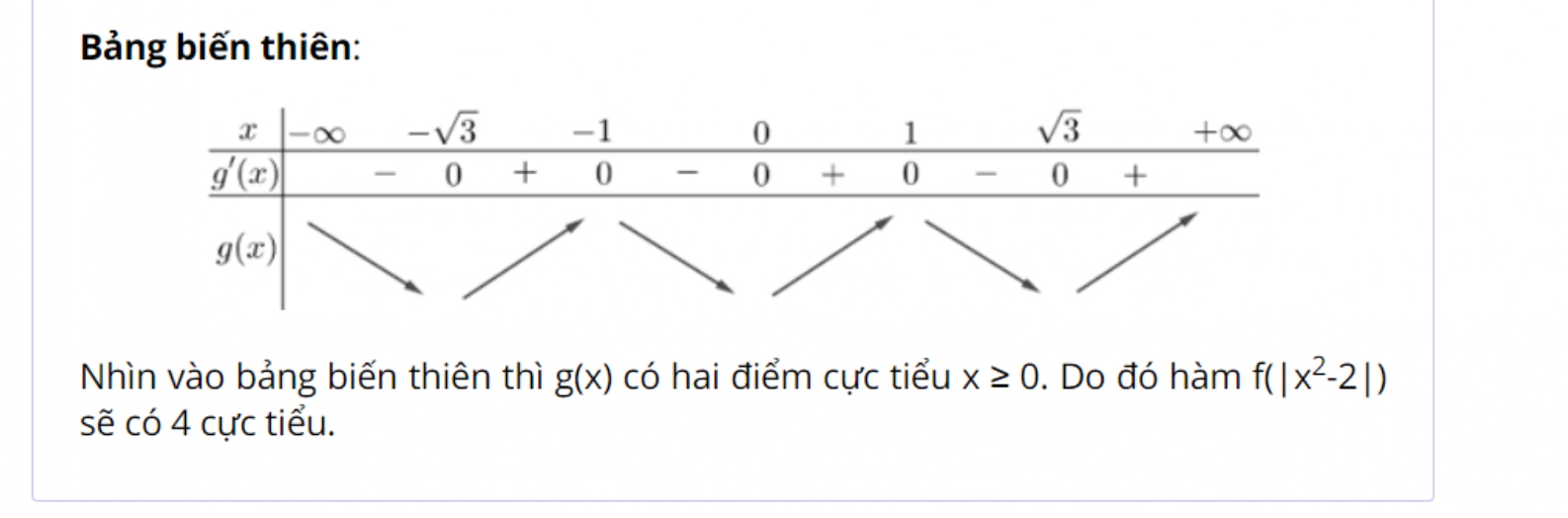
Xem thêm: what do you do for a living

*Ví dụ 10:

Trên đó là toàn cỗ kỹ năng tương quan cho tới dạng bài xích vô cùng trị của hàm trị vô cùng. Hy vọng trải qua nội dung bài viết bên trên những các bạn sẽ hiểu cách tiến hành và thuần thục dạng bài xích này, đơn giản và dễ dàng vận dụng vô quy trình ôn tập dượt kỹ năng và thực hiện bài xích đánh giá, bài xích đua.