hình hộp chữ nhật có bao nhiêu cạnh

Bách khoa toàn thư cởi Wikipedia

Bạn đang xem: hình hộp chữ nhật có bao nhiêu cạnh

"Góc" thay đổi phía sắp tới. Đối với những khái niệm không giống, coi Góc (định hướng).

Hình học
Hình chiếu một phía cầu lên trên bề mặt bằng phẳng.
Đại cương Lịch sử
Phân nhánh Euclid Phi Euclid Elliptic Cầu Hyperbol Hình học tập phi Archimedes Chiếu Afin Tổng hợp Giải tích Đại số Số học Diophantos Vi phân Riemann Symplectic Phức Hữu hạn Rời rạc Kỹ thuật số Lồi Tính toán Fractal Liên thuộc
Khái niệm Chiều Phép dựng hình bởi thước kẻ và compa Đỉnh Đường cong Đường chéo Góc Song song Vuông góc Đối xứng Đồng dạng Tương đẳng
Không chiều Điểm
Một chiều Đường thẳng Đoạn thẳng Tia Chiều dài
Hai chiều Mặt phẳng Diện tích Đa giác Tam giác Đường cao (tam giác) Cạnh huyền Định lý Pythagoras Hình bình hành Hình vuông Hình chữ nhật Hình thoi Rhomboid Tứ giác Hình thang Hình diều Đường tròn Đường kính Chu vi Diện tích
Ba chiều Thể tích Khối lập phương Hình vỏ hộp chữ nhật Hình trụ tròn Hình chóp Mặt cầu
Bốn chiều / số chiều khác Tesseract Siêu cầu
Nhà hình học
theo tên Aida Aryabhata Ahmes Alhazen Apollonius Archimedes Atiyah Baudhayana Bolyai Brahmagupta Cartan Coxeter Descartes Euclid Euler Gauss Gromov Hilbert Jyeṣṭhadeva Kātyāyana Khayyám Klein Lobachevsky Manava Minkowski Minggatu Pascal Pythagoras Parameshvara Poincaré Riemann Sakabe Sijzi al-Tusi Veblen Virasena Yang Hui al-Yasamin Trương Hành
theo giai đoạn trước Công nguyên Ahmes Baudhayana Manava Pythagoras Euclid Archimedes Apollonius 1–1400s Trương Hành Kātyāyana Aryabhata Brahmagupta Virasena Alhazen Sijzi Khayyám al-Yasamin al-Tusi Yang Hui Parameshvara 1400s–1700s Jyeṣṭhadeva Descartes Pascal Minggatu Euler Sakabe Aida 1700s–1900s Gauss Lobachevsky Bolyai Riemann Klein Poincaré Hilbert Minkowski Cartan Veblen Coxeter Ngày nay Atiyah Gromov
x t s

Trong hình học tập Euclid, góc là các thứ nằm trong lòng hai tuyến đường trực tiếp rời nhau bên trên một điểm. Hai đường thẳng liền mạch được gọi là cạnh của góc. Giao điểm của bọn chúng gọi là đỉnh của góc. Khi hai tuyến đường trực tiếp tuy vậy song cùng nhau, ko rời nhau bên trên điểm này (hoặc cũng rất có thể hiểu là rời nhau bên trên vô cực), góc đằm thắm bọn chúng bởi ko và không tồn tại đỉnh xác lập (hoặc đỉnh ở vô cực).

Nếu lấy một vòng tròn trặn đơn vị chức năng sở hữu tâm bên trên gửi gắm điểm O của hai tuyến đường trực tiếp và hai tuyến đường trực tiếp rời vòng tròn trặn đơn vị chức năng bên trên A₁, A₂ và B₁, B₂. Góc đằm thắm hai tuyến đường trực tiếp được xem là chừng nhiều năm cung nối đằm thắm A_i và B_j, với i và j bởi 1 hoặc 2 tùy từng quy ước, phân chia mang đến đơn vị chức năng chừng nhiều năm nhằm vô hiệu loại vẹn toàn và nhân với hằng số tỷ trọng tùy nằm trong vô đơn vị chức năng đo góc^{[cần dẫn nguồn]}.

Trong không khí thân phụ chiều, góc đằm thắm nhị mặt mũi phẳng (còn được gọi là góc khối) là phần không khí số lượng giới hạn bởi nhị mặt mũi bằng phẳng bại, được đo bởi góc đằm thắm hai tuyến đường trực tiếp bên trên nhị mặt mũi bằng phẳng nằm trong trực gửi gắm với gửi gắm tuyến của nhị mặt mũi bằng phẳng.

Khái niệm góc cũng khá được không ngừng mở rộng mang đến đại số tuyến tính. Để vô hiệu phiền nhiễu vô quy dự tính góc, rất có thể thay cho những đường thẳng liền mạch bởi những véctơ thể hiện tại không những chừng nghiêng mà còn phải cả phía. Khi tịnh tiến thủ những véctơ về nằm trong tâm O và lấy một vòng tròn trặn đơn vị chức năng bên trên tâm này, những véctơ tiếp tục chỉ rời vòng tròn trặn này bên trên nhị điểm A và B. Độ rộng lớn góc đằm thắm nhị véctơ được xem là chừng nhiều năm cung bên trên vòng tròn trặn nối A và B phân chia mang đến đơn vị chức năng chừng nhiều năm.

Dụng cụ đo góc[sửa | sửa mã nguồn]

Thước đo góc[sửa | sửa mã nguồn]

Người tao thông thường người sử dụng thước đo góc nhằm đo góc. Trên thước ghi những số đo kể từ 0 cho tới 180 theo gót 2 vòng cung ngược nhau nhằm việc đo góc được thuận tiện.

Giác kế[sửa | sửa mã nguồn]

Giác tiếp ngang[sửa | sửa mã nguồn]

Giác tiếp ngang dùng làm đo góc bên trên mặt mũi khu đất. Nó bao gồm một đĩa tròn trặn được đặt điều ở ngang bên trên giá chỉ 3 chân. Mặt đĩa tròn trặn được phân chia chừng sẵn. Trên mặt mũi đĩa sở hữu thanh xoay xung xung quanh tâm đĩa; 2 đầu thanh xoay sở hữu gắn 2 tấm trực tiếp đứng, từng tấm sở hữu một khe hở, 2 khe ở và tâm của đĩa luôn luôn trực tiếp sản phẩm.

Để đo một góc bên trên mặt mũi khu đất, tao đặt điều giác tiếp sao mang đến mặt mũi đĩa tròn trặn ở ngang và tâm của chính nó phía trên đường thẳng liền mạch đứng trải qua đỉnh của góc cần thiết đo. Sau đó:

1. Điều chỉnh thanh trở lại địa điểm 0, rồi bên cạnh đó kiểm soát và điều chỉnh mặt mũi đĩa và thanh xoay sao mang đến cạnh loại nhất của góc trực tiếp sản phẩm với 2 khe hở.
2. Giữ thắt chặt và cố định mặt mũi đĩa và fake thanh xoay sao mang đến cạnh loại nhị của góc trực tiếp sản phẩm với 2 khe hở. Số đo góc cần thiết mò mẫm đó là địa điểm nhưng mà thanh xoay chỉ vào sau cùng công đoạn này.

Giác tiếp đứng[sửa | sửa mã nguồn]

Giác tiếp đứng dùng làm đo góc theo gót phương trực tiếp đứng. Sở phận chủ yếu của giác tiếp đứng là thước đo góc rất có thể xoay quanh trục O cắm vuông góc với cọc PQ đặt tại địa điểm trực tiếp đứng. Tại 2 đầu của thước nom sở hữu gắn 2 cái đinh bên trên A và B. Tại O sở hữu treo chão dọi OF (trong hình b, E là vạch ứng với điểm 0 bên trên thước đo góc. Ta sở hữu góc phù hợp bởi OE và OF là góc tạo ra bởi phương nom và phương ở ngang)

Đơn vị đo lường và tính toán của góc[sửa | sửa mã nguồn]

Radian[sửa | sửa mã nguồn]

Trong hệ đo lường và tính toán quốc tế, góc được đo bởi radian. Một góc bẹt bởi π radian.

Độ[sửa | sửa mã nguồn]

Độ rộng lớn của một góc cũng khá được đo bởi đơn vị chức năng thông thườn là chừng, sở hữu ký hiệu là °. Một góc bẹt bởi 180 chừng.

Độ được tạo thành những đơn vị chức năng thấp rộng lớn là phút và giây

1 Độ = 60 phút. Phút kí hiệu là '

1 Phút = 60 giây. Giây kí hiệu là "

Vòng[sửa | sửa mã nguồn]

Vòng là 1 trong đơn vị chức năng đo có tính rộng lớn bởi 1 lối tròn trặn (360 độ).

Xem thêm: ai là người đặt tên cho dòng sông

Các loại góc[sửa | sửa mã nguồn]

• 

  Góc nhọn là góc to hơn 0° tuy nhiên nhỏ rộng lớn 90°

• 

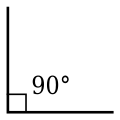
  Góc vuông là góc bởi 90° (1/4 vòng tròn);

• 

  Góc tù là góc to hơn 90° tuy nhiên nhỏ rộng lớn 180°

• 

  Góc bẹt là góc bởi 180° (1/2 vòng tròn).

• 

  Góc phản là góc to hơn 180° tuy nhiên nhỏ rộng lớn 360°

• 

  Góc ăm ắp là góc bởi 360° (toàn cỗ vòng tròn).

• 

• 

• 

  Chia song một góc bởi compa và thước kẻ

• 

Đại số tuyến tính[sửa | sửa mã nguồn]

Trong đại số tuyến tính; góc g; nằm trong lòng nhị véctơ, v₁ và v₂, được khái niệm qua loa phép tắc nhân vô vị trí hướng của nhị véctơ:

Với

"." là phép tắc nhân vô phía nhị vecto

|v_i| là sự cân đối của véctơ

cos(g) là hàm cos của góc g.

Khi nhị véctơ trực gửi gắm, góc đằm thắm bọn chúng là góc vuông, thì:

v₁. v₂ = 0

Tia phân giác[sửa | sửa mã nguồn]

Tia phân giác của góc là tia nằm trong lòng nhị cạnh của góc và tạo ra với nhị cạnh ấy nhị góc đều bằng nhau. Nó là quỹ tích của những điểm cơ hội đều nhị cạnh của góc. Bất kỳ điểm này phía trên tia phân giác đều cơ hội đều nhị tia bại.

Biến thay cho thế góc[sửa | sửa mã nguồn]

Giống như độ quý hiếm số, số đo góc cũng bại trở thành thế: α (alpha), β (beta), γ (gamma), δ (delta), ε (epsilon), ζ (zeta), η (eta), θ (theta), ι (iota), κ (kappa), Λ (lambda), μ (mu), ν (nu), ξ (xi), ο (omicron), ρ (rho), τ (tau), υ (upsilon), φ (phi), χ (chi), ψ (psi) và ω (omega).

Xem thêm: văn tả cái cặp lớp 5

Các đặc điểm của góc[sửa | sửa mã nguồn]

• Một tia cũng là 1 trong góc và sở hữu số đo là 0 chừng.
• Nếu tia OA nằm trong lòng Oz và Oy thì A trực thuộc góc zOy.
• Nếu tia Oa nằm trong lòng Ox và Oy thì: xOa + aOy = xOy.
• Tia phân giác Oa của góc xOy khi:

- Oa nằm trong lòng Ox và Oy (xOa + aOy = xOy)

- Hai góc được chia nhỏ ra bởi tia đều bằng nhau (xOa = aOy).

• Hai góc kề nhau là nhị góc sở hữu cạnh công cộng, nhị cạnh sót lại phía trên nhị nửa mặt mũi bằng phẳng đối nhau.
• Hai góc phụ nhau sở hữu tổng số đo bởi một góc vuông.
• Hai góc bù nhau sở hữu tổng số đo bởi một góc bẹt.
• Hai góc kề bù là nhị góc một vừa hai phải kề nhau một vừa hai phải bù nhau, sở hữu số đo bởi 1 góc bẹt
• Hai tia đối nhau tạo ra trở thành một góc bẹt.

- Các đường thẳng liền mạch đồng quy bên trên một điểm sẽ tạo nên đi ra những cặp 2 góc đối đỉnh nhau. 2 góc đối đỉnh nhau thì sở hữu nằm trong số đo.

Xem thêm[sửa | sửa mã nguồn]

• Góc khối
• Bài toán phân chia thân phụ một góc

Liên kết ngoài[sửa | sửa mã nguồn]

Wikimedia Commons được thêm hình hình ảnh và phương tiện đi lại truyền đạt về Góc.

• Góc bên trên Từ điển bách khoa Việt Nam
• Góc lượng giác bên trên Từ điển bách khoa Việt Nam
• Góc nhiều diện bên trên Từ điển bách khoa Việt Nam
• “Angle”. PlanetMath.

• Weisstein, Eric W., "Angle" kể từ MathWorld.

Chú thích[sửa | sửa mã nguồn]