
Chứng minh “Tứ giác nội tiếp” vô công tác Toán 9 là dạng bài bác tập luyện thông thườn, thông thường xuyên bắt gặp ở những bài bác đánh giá và kỳ ganh đua cần thiết. Để chung học viên bắt có thể kỹ năng và kĩ năng, thầy Nguyễn Quyết Thắng – Giáo viên môn Toán bên trên Hệ thống Giáo dục đào tạo HOCMAI tiếp tục triển khai bài bác giảng để giúp đỡ những em lấy hoàn hảo điểm phần này. Hãy nằm trong dò xét hiểu!
Bạn đang xem: các cách chứng minh tứ giác nội tiếp
Chứng minh tứ giác nội tiếp là tao cần thiết minh chứng 4 đỉnh của tứ giác phía trên và một đàng tròn trĩnh. Dạng bài bác tập luyện này sẽ sở hữu nhiều cường độ nhằm thách thức những em học viên kể từ tầm cho tới xuất sắc vô công tác Toán lớp 9. Trong quy trình học tập và theo dõi dõi bài bác, người học tập nên triệu tập cao phỏng, biên chép không thiếu thốn nhằm học hành hiệu suất cao.
Tham khảo thêm:
Cách minh chứng 2 tam giác đồng dạng
Cách xác lập tâm đàng tròn trĩnh nước ngoài tiếp
Một số kỹ năng cần thiết về tứ giác nội tiếp
-
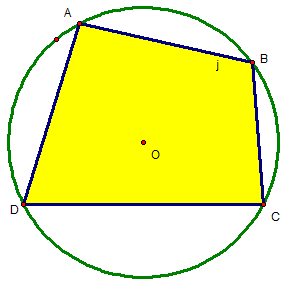
- Định nghĩa: Một tứ giác đem tứ đỉnh nằm trong phía trên một đàng tròn trĩnh gọi là tứ giác nội tiếp đàng tròn trĩnh.
- Định lý: Trong một tứ giác nội tiếp, tổng số đo nhị góc đối lập bởi vì 180 phỏng.
- Định lý đảo: Nếu một tứ giác đem tổng số đo nhị góc đối lập bởi vì 180 phỏng thì tứ giác ê nội tiếp được đàng tròn trĩnh.
- Ngoài rời khỏi, tao còn tồn tại một trong những hệ quả:
– Hai góc nội tiếp nằm trong chắn một cung thì đều nhau.
– Góc nội tiếp bởi vì nửa góc ở tâm nằm trong chắn một cung.
– Góc tạo ra bởi vì tiếp tuyến và chạc cung bởi vì góc nội tiếp nằm trong chắn một cung.
Phương pháp số 1: Chứng minh tứ giác đem tổng nhị góc đối bởi vì 180 độ
Phương pháp này được xuất phát điểm từ chủ yếu khái niệm của tứ giác nội tiếp. Nội dung của cách thức này như sau:“Nếu tứ giác ABCD đem tổng nhị góc đối bởi vì 180 phỏng thì tứ giác ê nội tiếp”
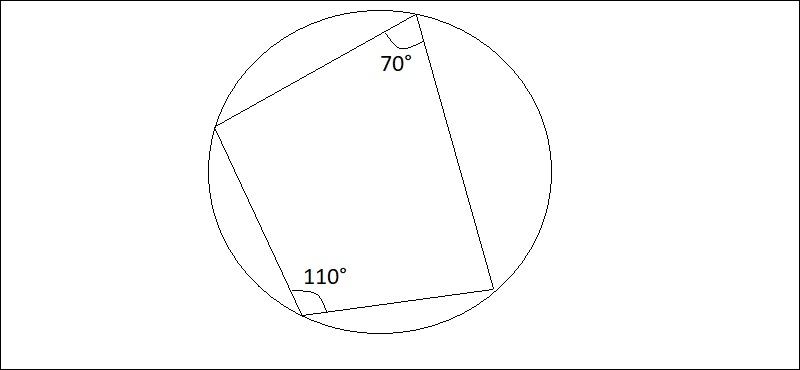
Hệ trái ngược của nội dung này là:
Cho tứ giác ABCD:
- Nếu BAD = BCD = 90 độ thì tứ giác ABCD nội tiếp đàng tròn trĩnh tâm O 2 lần bán kính BD
- Nếu tổng nhị góc kề bù EAD = BCD thì tứ giác ABCD nội tiếp
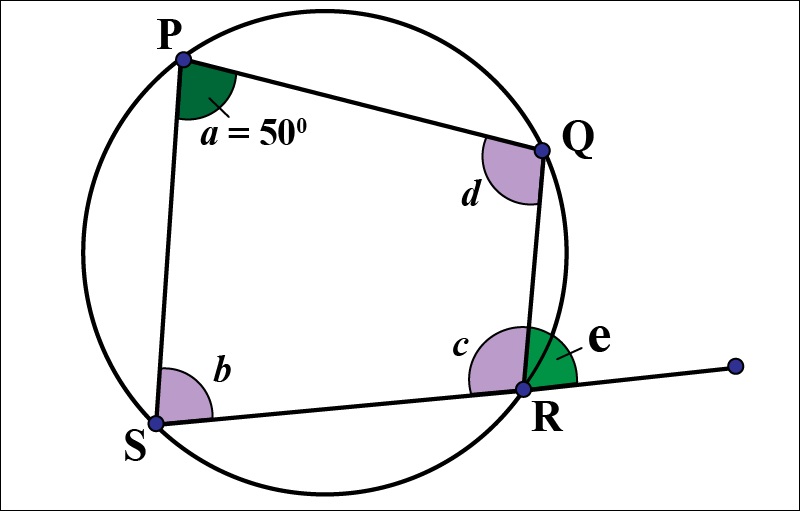
Phương pháp số 2: Chứng minh tứ giác đem góc ngoài bên trên một đỉnh bởi vì góc vô của đỉnh đối diện
Ở cách thức này, học viên lưu ý cần nhìn chính hình chính góc, còn nếu như không có khả năng sẽ bị hiện tượng minh chứng sai tuy nhiên thành quả chính và tác động cho tới những câu tiếp sau. Cụ thể, khi đề bài bác cho tới tứ giác ABCD và minh chứng được góc ngoài bên trên đỉnh A bởi vì góc C của tứ giác (góc A và góc C đối đỉnh) thì hoàn toàn có thể Kết luận tứ giác ABCD là tứ giác nội tiếp.
Xem thêm: Tiến lên miền Nam iOS - Tải Game Miễn Phí, Kiếm Thưởng Liền Tay
Phương pháp số 3: Chứng minh nhị đỉnh nằm trong kề một cạnh, nằm trong nhìn cạnh ê bên dưới nhị góc đều nhau và bởi vì 90 độ
Phương pháp này vận dụng khi đề bài bác cho tới tứ giác ABCD và những dữ khiếu nại khêu gợi ý tính được rằng DAC = DBC = 90 phỏng. Từ ê, học viên hoàn toàn có thể Kết luận tứ giác ABCD nội tiếp đàng tròn trĩnh.
Phương pháp số 4: Chứng minh tứ đỉnh của một tứ giác cơ hội đều một điểm xác định
Nếu đề bài bác cho tới trước một đàng tròn trĩnh tâm O đem nửa đường kính R thì ngẫu nhiên điểm nào là phía trên đàng tròn trĩnh đều cơ hội tâm một khoảng chừng chính bởi vì nửa đường kính. Theo thầy Thắng chỉ dẫn, phụ thuộc đặc điểm này, học viên hoàn toàn có thể dễ dàng và đơn giản minh chứng một tứ giác nội tiếp một đàng tròn trĩnh.
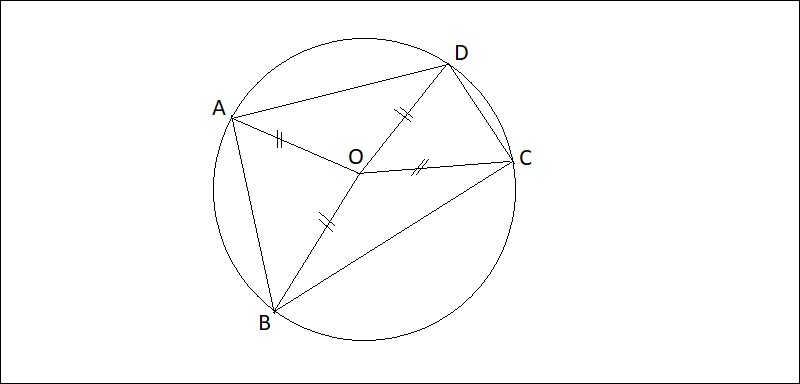
Ví dụ: Cho một điểm O thắt chặt và cố định và tứ giác ABCD.
Nếu học viên minh chứng được tứ điểm A, B, C, D cơ hội đều điểm O với khoảng cách bởi vì R, tức OA = OB = OC = OD = R thì điểm O đó là tâm đàng tròn trĩnh trải qua tứ điểm A, B, C, D. Hay thưa cách tiếp, tứ giác ABCD nội tiếp đàng tròn trĩnh tâm O nửa đường kính R.
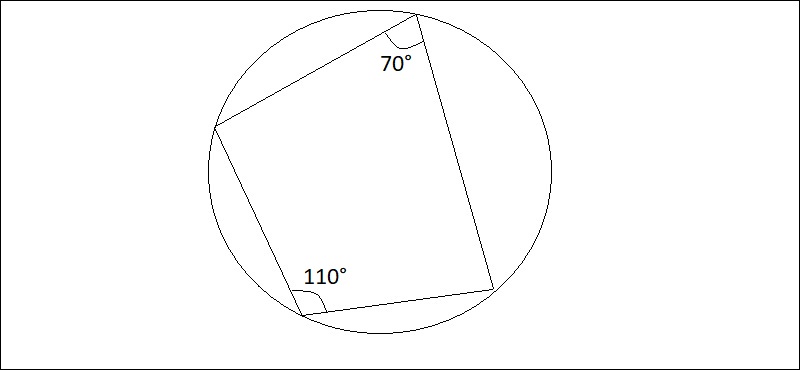
Phương pháp số 5: Tứ giác đem tổng số đo nhị cặp góc đối đều nhau thì tứ giác ê nội tiếp đàng tròn
Trong cách thức này, những em học viên hoàn toàn có thể minh chứng tổng số đo 2 góc đối bởi vì 180 phỏng thì hoàn toàn có thể thể hiện Kết luận tứ giác ê nội tiếp đàng tròn trĩnh.
Ví dụ: Cho một tứ giác tứ giác ABCD
Để ABCD là tứ giác nội tiếp đàng tròn trĩnh ⇔ góc A + góc C = góc B + góc D. Trong tình huống quan trọng đặc biệt tổng những góc đối bởi vì 180 phỏng tao đã có được hệ trái ngược là cách thức số 1.
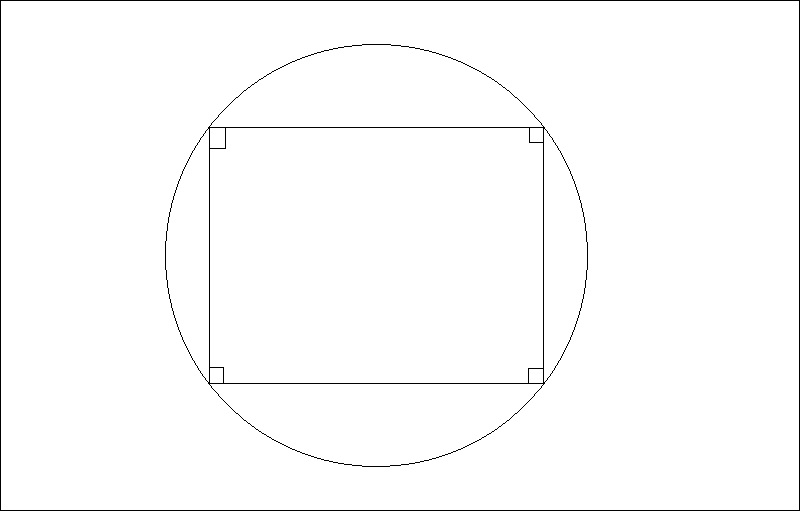
Phương pháp số 6: Chứng minh tứ giác nằm trong dạng tứ giác đặc biệt
Với cách thức này, những em học viên hãy minh chứng tứ giác đề bài bác tiếp tục cho rằng tứ giác đem dạng hình vuông vắn, hình chữ nhật, hình thoi hoặc hình bình hành,… rồi kể từ ê suy rời khỏi tứ giác tiếp tục cho rằng tứ giác nội tiếp.
Xem thêm: điểm chuẩn đại học nha trang 2022
Một số cảnh báo khi thực hiện bài bác minh chứng tứ giác nội tiếp
- Học sinh nên vẽ hình rõ rệt, xinh xắn và tách vẽ hình bên trên một trong những tình huống quan trọng đặc biệt.
- Các kí hiệu góc, đoạn trực tiếp đều nhau rất cần phải ghi lại rõ rệt.
- Bám vô fake thiết, kỹ năng tiếp tục học tập nhằm thực hiện bài bác cho tới hiệu suất cao.
- Những đòi hỏi của đề bài bác cũng hoàn toàn có thể là phía khêu gợi ý nhằm giải quyết và xử lý vấn đề.
- Không người sử dụng những điều đang được cần thiết minh chứng nhằm minh chứng lại bọn chúng.
Trên đó là 4 cách thức và những cảnh báo chung học viên minh chứng tứ giác nội tiếp giản dị và đơn giản, hiệu suất cao rộng lớn. Các em lưu ý theo dõi dõi bài bác giảng và biên chép không thiếu thốn nhằm nắm rõ kỹ năng và vận dụng vô bài bác tập luyện. Đồng thời, bố mẹ mong muốn chung con cái ôn tập luyện môn Toán cho tới kỳ ganh đua thời điểm cuối năm và luyện ganh đua vô 10 hiệu suất cao, hoàn toàn có thể ĐK cho tới con cái một khóa đào tạo online tận nơi nhằm tiết kiệm chi phí thời hạn học tập tăng ở ngoài.
Tự hào là nền tảng học tập trực tuyến số 1 giành riêng cho học viên phổ thông VN, lúc này Hệ thống Giáo dục đào tạo HOCMAI đang được lên kế hoạch Chương trình Học chất lượng 2020-2021 nhằm mục đích mục tiêu chung học viên bên trên toàn nước tiếp cận với kho tư liệu và bài bác giảng unique tới từ những thầy thầy giáo có không ít năm tay nghề trong lĩnh vực. Hãy nhập cuộc công tác tức thì thời điểm hôm nay nhằm thỏa sức tự tin rộng lớn và đột phá vô học tập tập!











.png)
Bình luận