Chủ đề tình huống đều bằng nhau của tam giác vuông: Tam giác vuông có không ít tình huống đều bằng nhau, điều này tạo cho tam giác vuông trở thành thú vị và nhiều chủng loại. Có nhị tình huống cần thiết nhằm chú ý là lúc nhị cạnh góc vuông của tam giác vuông đều bằng nhau và khi cạnh góc vuông và góc nhọn kề cạnh này cũng đều bằng nhau. Việc dò la hiểu và vận dụng những tình huống này gom tất cả chúng ta làm rõ rộng lớn về đặc thù quan trọng đặc biệt của tam giác vuông và giải quyết và xử lý những việc tương quan cho tới nó một cơ hội đơn giản.
Có những tình huống này khiến cho nhị tam giác vuông trở thành bởi vì nhau?
Có những tình huống thực hiện mang lại nhị tam giác vuông trở thành bởi vì nhau:
1. Trường thích hợp 1: Hai cạnh góc vuông của nhị tam giác vuông đều bằng nhau. Như vậy Có nghĩa là nhị tam giác vuông có tính lâu năm nhị cạnh góc vuông đều đều bằng nhau.
2. Trường thích hợp 2: Một cạnh góc vuông và một góc nhọn kề cạnh bại liệt của nhị tam giác vuông đều bằng nhau. Như vậy Có nghĩa là nhị tam giác vuông sở hữu một cạnh góc vuông và một góc nhọn kề cạnh bại liệt có tính lâu năm đều bằng nhau.
3. Trường thích hợp 3: Cạnh huyền và một cạnh góc vuông của nhị tam giác vuông đều bằng nhau. Như vậy Có nghĩa là nhị tam giác vuông sở hữu cạnh huyền và một cạnh góc vuông có tính lâu năm đều bằng nhau.
Để xác nhận rằng nhị tam giác vuông đều bằng nhau, tao cần thiết xác minh rằng những cạnh và góc ứng của nhị tam giác đã và đang được chỉ định và hướng dẫn trong những tình huống bên trên đều đều bằng nhau.
Bạn đang xem: các trường hợp bằng nhau của tam giác vuông
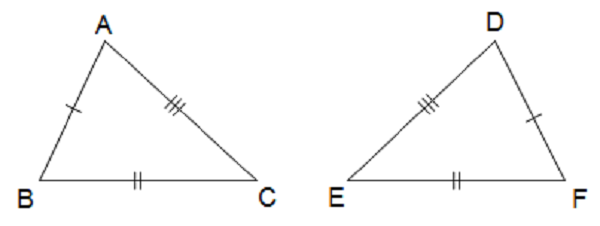
Trường thích hợp này khi nhị tam giác vuông sẽ là bởi vì nhau?
Trường thích hợp khi nhị tam giác vuông sẽ là đều bằng nhau là lúc những cạnh góc vuông và cạnh huyền của nhị tam giác vuông này đều bằng nhau.
Cụ thể, sở hữu nhị tình huống khi nhị tam giác vuông sẽ là bởi vì nhau:
Trường thích hợp 1: Hai cạnh góc vuông của nhị tam giác vuông bởi vì nhau: Trong tình huống này, nhị tam giác vuông sẽ sở hữu được nhị cạnh góc vuông có tính lâu năm đều bằng nhau.
Trường thích hợp 2: Cạnh góc vuông và góc nhọn kề cạnh góc vuông của nhị tam giác vuông bởi vì nhau: Trong tình huống này, một cạnh góc vuông của tam giác vuông thứ nhất và góc nhọn kề cạnh góc vuông này cũng bởi vì cạnh ứng của tam giác vuông loại nhị.
Khi nhị tam giác vuông thỏa mãn nhu cầu 1 trong những nhị tình huống bên trên, bọn chúng sẽ là đều bằng nhau. Như vậy đồng nghĩa tương quan với việc những góc, cạnh và cạnh huyền ứng của nhị tam giác vuông đều bằng nhau.
Có từng nào tình huống đều bằng nhau của tam giác vuông?
Có nhị tình huống đều bằng nhau của tam giác vuông.
1. Trường thích hợp 1: Hai cạnh góc vuông của nhị tam giác vuông đều bằng nhau.
2. Trường thích hợp 2: Một cạnh góc vuông và cạnh kề góc vuông của nhị tam giác vuông đều bằng nhau.
Tam giác vuông - Bài 8 - Toán học tập 7 - Cô Nguyễn Anh (HAY NHẤT)
Tại sao tình huống đều bằng nhau lại cần thiết nhập toán học? Video này tiếp tục lý giải một cơ hội rõ nét và sáng tỏ, khiến cho bạn hiểu trúng và vận dụng công thức một cơ hội đúng chuẩn. Hãy coi tức thì nhằm nắm rõ loài kiến thức!
Tam giác vuông đều bằng nhau khi nào?
Tam giác vuông đều bằng nhau khi nhị tam giác vuông này còn có nằm trong cạnh huyền và và một cạnh góc vuông.
Cụ thể, sở hữu nhị tình huống khi tam giác vuông bởi vì nhau:
1. Trường thích hợp 1: Hai tam giác vuông sở hữu cạnh góc vuông chung:
- Nếu nhị tam giác vuông sở hữu cạnh góc vuông cộng đồng, tức là 1 trong cạnh góc vuông và một cạnh huyền của tam giác vuông này bởi vì một cạnh góc vuông và một cạnh huyền của tam giác vuông bại liệt, thì nhị tam giác vuông bại liệt đều bằng nhau.
2. Trường thích hợp 2: Hai tam giác vuông sở hữu cạnh góc vuông ko cộng đồng tuy nhiên cạnh huyền chung:
- Nếu nhị tam giác vuông sở hữu cạnh huyền cộng đồng, tức là cạnh huyền và một cạnh góc vuông của tam giác vuông này bởi vì cạnh huyền và một cạnh góc vuông của tam giác vuông bại liệt, thì nhị tam giác vuông bại liệt đều bằng nhau.
Đó là cơ hội xác lập lúc nào nhị tam giác vuông đều bằng nhau dựa vào cạnh huyền và cạnh góc vuông của bọn chúng.
Tam giác vuông đều bằng nhau sở hữu những Điểm lưu ý gì?
Tam giác vuông đều bằng nhau sở hữu những Điểm lưu ý sau:
1. Hai tam giác vuông được gọi là đều bằng nhau nếu như một cạnh của góc vuông và cạnh huyền của tam giác vuông này bởi vì một cạnh của góc vuông và cạnh huyền của tam giác vuông bại liệt.
2. Trường thích hợp 1: Hai tam giác vuông sở hữu nhị cạnh góc vuông đều bằng nhau (đối đối với cả nhị góc vuông).
3. Trường thích hợp 2: Hai tam giác vuông sở hữu một cạnh góc vuông và góc nhọn kề cạnh bại liệt đều bằng nhau.
4. Hai tam giác vuông đều bằng nhau cũng đều có những cặp cạnh ứng đều bằng nhau, chính vì cạnh huyền của tam giác vuông đó là cạnh lớn số 1 và đối lập với góc vuông.
_HOOK_
Tam giác vuông - Phần 1 - Toán 7 - OLM.VN
Bạn đang được học tập toán học tập lớp 7 và ham muốn nâng cấp kĩ năng của mình? Video này tiếp tục cung ứng những bài xích giảng và ví dụ thực tiễn khiến cho bạn làm rõ rộng lớn về những chủ thể phức tạp như hình học tập, cách thức giải toán. Hãy nằm trong học tập và vượt lên những thách thức!
Xem thêm: sách giáo khoa cánh diều
Các tình huống đều bằng nhau của tam giác vuông khi sở hữu cạnh góc vuông và góc nhọn là gì?
Các tình huống đều bằng nhau của tam giác vuông khi sở hữu cạnh góc vuông và góc nhọn là như sau:
1. Trường thích hợp 1: Hai cạnh góc vuông đều bằng nhau.
Khi nhị tam giác vuông sở hữu cạnh góc vuông đều bằng nhau, tao sở hữu tam giác vuông này là đều bằng nhau.
2. Trường thích hợp 2: Cạnh góc vuông và góc nhọn kề cạnh bại liệt đều bằng nhau.
Khi nhị tam giác vuông sở hữu cạnh góc vuông và góc nhọn kề cạnh bại liệt đều bằng nhau, tao sở hữu tam giác vuông này là đều bằng nhau.
Ví dụ:
Cho nhị tam giác vuông ABC và DEF. Ta biết AB = DE và góc A = góc D. Khi bại liệt, tam giác ABC và tam giác DEF là đều bằng nhau.
Đây là những tình huống cơ phiên bản nhằm xác lập nhị tam giác vuông sở hữu đều bằng nhau hay là không, dựa vào đặc thù của cạnh góc vuông và góc nhọn.
Trường thích hợp này là tình huống một trong các các trường hợp bằng nhau của tam giác vuông?
Trường thích hợp một trong các các trường hợp bằng nhau của tam giác vuông là lúc nhị tam giác vuông sở hữu nhị cạnh góc vuông đều bằng nhau. Để tình huống này xẩy ra, tao cần thiết đối chiếu phỏng lâu năm nhị cạnh góc vuông của nhị tam giác và xác lập coi bọn chúng sở hữu đều bằng nhau ko. Nếu nhị cạnh góc vuông của nhị tam giác có tính lâu năm như nhau, tức là cạnh này của tam giác loại nhất có tính lâu năm bởi vì cạnh ứng của tam giác loại nhị, thì bại liệt đó là tình huống một trong các các trường hợp bằng nhau của tam giác vuông.

Trong tình huống 2, tam giác vuông đều bằng nhau khi sở hữu cạnh góc vuông và góc nhọn kề cạnh bại liệt như vậy nào?
Trong tình huống 2 của tam giác vuông đều bằng nhau, tất cả chúng ta sở hữu một cạnh góc vuông và góc nhọn kề cạnh bại liệt. Để tam giác vuông đều bằng nhau, cạnh góc vuông và góc nhọn kề cạnh bại liệt của nhị tam giác cần được tương tự.
Để xác lập nhị tam giác sở hữu tương tự hay là không, tất cả chúng ta cần thiết đối chiếu những nhân tố sau:
1. Cạnh góc vuông: Hai tam giác cần phải có cạnh góc vuông đều bằng nhau. Như vậy Có nghĩa là cạnh góc vuông của tam giác A nên bởi vì cạnh góc vuông của tam giác B.
2. Góc nhọn kề cạnh đó: Cả nhị tam giác cần phải có góc nhọn kề cạnh bại liệt tương tự. Như vậy Có nghĩa là góc nhọn kề cạnh bại liệt của tam giác A nên bởi vì góc nhọn kề cạnh bại liệt của tam giác B.
Nếu cả nhị nhân tố này đều thoả mãn, tức là cạnh góc vuông và góc nhọn kề cạnh bại liệt của nhị tam giác đều bằng nhau, thì tao hoàn toàn có thể Kết luận rằng nhị tam giác này là tương tự và đều bằng nhau.
Ví dụ:
Tam giác A sở hữu cạnh góc vuông AB và góc nhọn kề cạnh bại liệt AC.
Tam giác B sở hữu cạnh góc vuông DE và góc nhọn kề cạnh bại liệt DF.
Nếu AB = DE và AC = DF, thì tao hoàn toàn có thể Kết luận rằng tam giác A và tam giác B là tương tự và đều bằng nhau.
Tam giác vuông - Bài 8 - Toán học tập 7 - Cô Nguyễn Thu Hà (DỄ HIỂU NHẤT)
Cô Nguyễn Anh là 1 trong nhà giáo toán tài năng và hăng hái. Video này tiếp tục mang về những bài xích giảng trải qua cách thức giảng dạy dỗ lạ mắt của cô ý. Hãy lắng tai những điều giảng kể từ cô nhằm thâu tóm kiến thức và kỹ năng một cơ hội đơn giản và thú vị!
Cách đánh giá và minh chứng nhị tam giác vuông đều bằng nhau như vậy nào?
Để đánh giá và minh chứng nhị tam giác vuông đều bằng nhau, tất cả chúng ta hoàn toàn có thể dùng một trong mỗi cơ hội sau:
Cách 1: Sử dụng qui định vấp ngã đề. Để thực hiện điều này, tất cả chúng ta cần thiết minh chứng rằng nhị tam giác vuông sở hữu và một cặp cạnh góc vuông và cạnh huyền. Cụ thể, tao hoàn toàn có thể tiến hành quá trình sau:
Bước 1: Xác tấp tểnh những cặp cạnh góc vuông và cạnh huyền của nhị tam giác vuông cần thiết minh chứng.
Bước 2: So sánh những cặp cạnh góc vuông và cạnh huyền của nhị tam giác. Nếu bọn chúng đều bằng nhau, tao hoàn toàn có thể Kết luận nhị tam giác vuông bại liệt đều bằng nhau.
Cách 2: Sử dụng giải tích hình học tập. Đối với tình huống này, tất cả chúng ta cần thiết minh chứng rằng những góc và phỏng lâu năm những cạnh của nhị tam giác vuông đều bằng nhau.
Bước 1: Gán độ quý hiếm cho những đỉnh của nhị tam giác vuông.
Bước 2: Tính toán những góc và phỏng lâu năm những cạnh của tất cả nhị tam giác.
Bước 3: So sánh những góc và phỏng lâu năm những cạnh của nhị tam giác. Nếu bọn chúng đều bằng nhau, tao hoàn toàn có thể Kết luận nhị tam giác vuông bại liệt đều bằng nhau.
Đối đối với cả nhị cơ hội bên trên, tất cả chúng ta cần thiết để ý đảm nói rằng toàn bộ những độ quý hiếm được xem toán và đối chiếu đều đúng chuẩn. Nếu những độ quý hiếm tương đương nhau, tao hoàn toàn có thể Kết luận rằng những tam giác vuông là đều bằng nhau.
Xem thêm: khủng hoảng kinh tế 1929 đến 1933

Tại sao việc hiểu về những tình huống đều bằng nhau của tam giác vuông cần thiết nhập học tập hình học?
Việc hiểu về những tình huống đều bằng nhau của tam giác vuông là đặc biệt cần thiết nhập học tập hình học tập vì thế nó gom tất cả chúng ta thấy được côn trùng tương tác Một trong những Điểm lưu ý và đặc thù của những tam giác vuông không giống nhau.
1. Trường thích hợp cạnh góc vuông: Khi nhị tam giác vuông sở hữu cạnh góc vuông đều bằng nhau, tao hoàn toàn có thể Kết luận rằng những cạnh sót lại cũng tiếp tục đều bằng nhau. Như vậy thể hiện một quy tắc cần thiết nhập hình học tập là: \"Hai tam giác vuông sở hữu một cặp cạnh đều bằng nhau thì những cặp cạnh sót lại cũng đều bằng nhau.\"
2. Trường thích hợp cạnh góc vuông và góc nhọn kề cạnh đó: Nếu một cạnh góc vuông và góc nhọn kề cạnh bại liệt của nhị tam giác vuông đều bằng nhau, tao hoàn toàn có thể Kết luận rằng tam giác vuông này cũng đều bằng nhau. Như vậy được cho phép tất cả chúng ta vận dụng quy tắc về những đàng cao, trung tuyến, đàng tầm và những nhân tố không giống nhập tam giác vuông.
3. Trường thích hợp cạnh huyền và cạnh góc vuông: Nếu cạnh huyền và một cạnh góc vuông của nhị tam giác vuông đều bằng nhau, thì tao hoàn toàn có thể Kết luận rằng những tam giác vuông bại liệt đều bằng nhau. Như vậy gom tất cả chúng ta xác lập những cặp góc đều bằng nhau và ĐK chắc chắn trong những tam giác vuông.
Bằng cơ hội nắm rõ những tình huống đều bằng nhau này, tất cả chúng ta hoàn toàn có thể vận dụng những cách thức, công thức và tấp tểnh lý nhằm giải quyết và xử lý những bài xích tập luyện và yếu tố tương quan cho tới tam giác vuông. Trong khi, việc hiểu sâu sắc về những tình huống này còn hoàn toàn có thể gom tất cả chúng ta cách tân và phát triển năng lực suy nghĩ, logic và giải quyết và xử lý yếu tố nhập hình học tập.
_HOOK_









Bình luận