cách tính tổng dãy số

Công thức tính tổng mặt hàng số cơ hội đều và ko cơ hội đều được thật nhiều người hâm mộ dò la kiếm vô thời khắc thời điểm hiện tại. Cả nhị đều là công thức cần thiết, đòi hỏi học viên làm rõ quy luật tạo hình của mặt hàng số nhằm hoàn toàn có thể vận dụng hiệu suất cao. Trong nội dung bài viết này, Hoàng Hà Mobile tiếp tục khiến cho bạn làm rõ rộng lớn về cả nhị công thức này kèm cặp ví dụ minh họa dễ dàng nắm bắt nhất.

Bài toán tính tổng mặt hàng số là gì?

Trước Khi dò la làm rõ rộng lớn về những công thức tính tổng mặt hàng số cơ hội đều và ko cơ hội đều, tất cả chúng ta nên làm rõ vấn đề tính tổng mặt hàng số là gì. Về cơ bạn dạng, vấn đề tính tổng một mặt hàng số là sự việc tính tổng những độ quý hiếm số học tập vô một chuỗi hoặc mặt hàng số ví dụ. Dãy số hoàn toàn có thể bao hàm những số nguyên vẹn, số thực, hoặc những loại số không giống, và hoàn toàn có thể được xác lập theo dõi một quy tắc chắc chắn hoặc giản dị là 1 trong list số mang đến trước.

Bạn đang xem: cách tính tổng dãy số

Có nhiều phương pháp để tính tổng này, tùy nằm trong vô loại mặt hàng số và mục tiêu sử dụng:

Tổng trực tiếp: Đây là cơ hội giản dị nhất, này đó là chúng ta nằm trong từng số vô mặt hàng lại cùng nhau. Ví dụ, tổng của mặt hàng số 1, 2, 3, 4 là 1 trong những + 2 + 3 + 4 = 10.

Công thức tổng quát: Đối với một vài mặt hàng số quan trọng đặc biệt (như mặt hàng số cung cấp số nằm trong hoặc cung cấp số nhân), hoàn toàn có thể dùng công thức toán học tập nhằm tính tổng nhưng mà không nhất thiết phải nằm trong từng số. Ví dụ, tổng của mặt hàng số cung cấp số nằm trong từ là 1 cho tới n là (n * (n + 1)) / 2.

Sử dụng lập trình: Trong lập trình sẵn PC, hoàn toàn có thể dùng vòng lặp nhằm tính tổng mặt hàng số. Đây là cách thức phổ cập Khi xử lý tài liệu số.

Phương pháp vận dụng tính tổng một mặt hàng số hiệu quả

Các cách thức sau đây tiếp tục khiến cho bạn đơn giản và dễ dàng giải những vấn đề tương quan cho tới tính tổng một mặt hàng số Khi vận dụng công thức tính tổng mặt hàng số cơ hội đều hoặc ko cơ hội đều. Để giải quyết và xử lý vấn đề tính tổng một mặt hàng số, trước không còn tao cần thiết làm rõ quy luật của mặt hàng số cơ. Dựa vô quy luật, tao hoàn toàn có thể xác lập phương pháp tính tổng một cơ hội đúng mực và hiệu suất cao.

Dưới đó là một vài quy luật phổ cập cùng theo với cơ hội tiếp cận nhằm tính tổng:

Cấp số cộng: Mỗi số hạng sau ngay số hạng trước thêm vào đó một vài bất ngờ a. Ví dụ: 2, 4, 6, 8,… ở phía trên a = 2. Tổng hoàn toàn có thể được xem nhanh chóng bởi công thức quan trọng đặc biệt của cung cấp số nằm trong.

Cấp số nhân: Mỗi số hạng sau ngay số hạng trước nhân với một vài bất ngờ q không giống 0. Ví dụ: 3, 9, 27, 81,… ở phía trên q = 3. Tổng cũng có thể có công thức riêng rẽ giành cho cung cấp số nhân.

Dãy số Fibonacci: Mỗi số hạng kể từ loại 3 trở lên đường bởi tổng nhị số hạng ngay lập tức trước. Ví dụ: 1, 1, 2, 3, 5, 8,… Tổng được xem bằng phương pháp nằm trong từng số hạng.

Quy luật tổng hợp: Có những quy luật phức tạp rộng lớn, như từng số hạng bởi tổng của số hạng trước cùng theo với một vài bất ngờ d và số trật tự của chính nó. Ví dụ: 2, 5, 9, 14,… ở phía trên d = 2.

Nhân với số loại tự: Mỗi số hạng sau ngay số hạng trước nhân với số trật tự của chính nó. Ví dụ: 2, 4, 12, 48,… ở phía trên số hạng trước tiên là 2.

Khi mình muốn tính tổng một mặt hàng số cơ hội đều, đó là phương thức giản dị và thú vị nhưng mà bạn cũng có thể thử:

Tính số số hạng xuất hiện tại vô dãy

Chúng tao chính thức bằng sự việc dò la đi ra đem từng nào số vô mặt hàng. Công thức như sau:

Số Số Hạng = (Số Hạng Cuối – Số Hạng Đầu) / Đơn Vị Khoảng Cách + 1

Ví dụ: Xét mặt hàng số từ là 1 cho tới 100. Số số hạng là (100 – 1) / 1 + 1 = 100.

Tính tổng mang đến mặt hàng số cơ hội đều nhau

Bây giờ, nhằm tính tổng, tao dùng công thức:

Tổng Dãy Số = (Số Hạng Đầu + Số Hạng Cuối) x Số Số Hạng / 2

Ví dụ: Với mặt hàng số kể từ 2 cho tới 50 cơ hội đều 2 đơn vị chức năng, tổng là (2 + 50) x 25 / 2 = 650.

Tìm số hạng cuối

Nếu chúng ta biết số hạng đầu và con số số hạng, bạn cũng có thể dò la số hạng cuối:

Số Hạng Cuối = Số Hạng Đầu + (Số Số Hạng – 1) x Đơn Vị Khoảng Cách

Ví dụ: Trong mặt hàng số 1, 3, 5,… đem 25 số hạng, số cuối là 1 trong những + (25 – 1) x 2 = 49.

Tìm số hạng đầu Khi vận dụng công thức tính tổng mặt hàng số cơ hội đều

Ngược lại, nếu như biết số hạng cuối và con số số hạng, bạn cũng có thể dò la số hạng đầu:

Số Hạng Đầu = Số Hạng Cuối – (Số Số Hạng – 1) x Đơn Vị Khoảng Cách

Ví dụ: Nếu mặt hàng số đem 50 số hạng, số cuối là 100 và khoảng cách là 2, số đầu là 100 – (50 – 1) x 2 = 2.

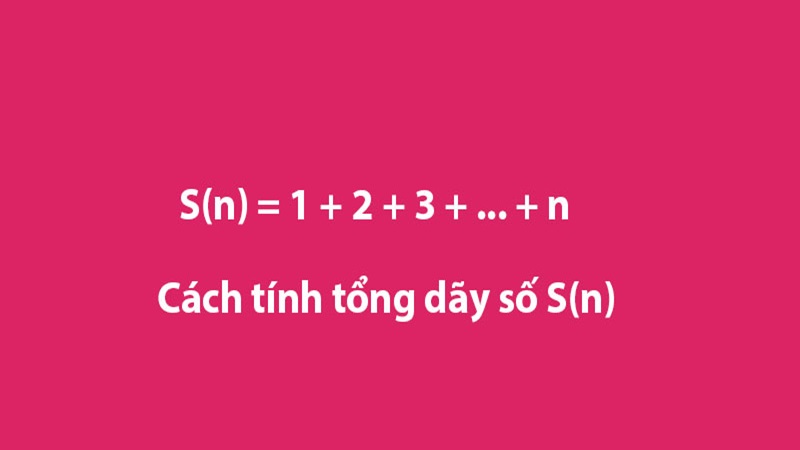
Tính khoảng cộng

Đôi Khi mình muốn biết khoảng của mặt hàng số thì đó là cơ hội nhưng mà bạn cũng có thể thực hiện:

Trung Bình Cộng = Tổng Dãy Số / Số Số Hạng

Ví dụ: Trung bình nằm trong của mặt hàng số từ là 1 cho tới 100 là 5050 / 100 = 50.5.

Lưu ý Khi áp dụng

Các công thức tính tổng mặt hàng số cơ hội đều bên trên khiến cho bạn nhanh gọn lẹ dò la đi ra đáp số nhưng mà không nhất thiết phải nằm trong từng số một, tiết kiệm chi phí thời hạn và công sức của con người, quan trọng đặc biệt hữu ích Khi thao tác với mặt hàng số lâu năm. Tuy nhiên cũng có thể có một vài Note nhưng mà bạn phải nắm vững như:

• Đầu tiên, hãy lưu giữ rằng bạn phải xác lập phụ vương nguyên tố chính: số hạng đầu, số hạng cuối, và tổng số số hạng vô mặt hàng. Đừng quên cả khoảng cách thân thiện nhị số thường xuyên.
• Nếu mặt hàng số của công ty đem con số số hạng là số lẻ, các bạn sẽ thấy rằng số hạng ở thân thiện hoàn toàn có thể tính được đơn giản và dễ dàng. Công thức là (số cuối + số đầu) / 2. Như vậy khiến cho bạn nhanh gọn lẹ dò la đi ra độ quý hiếm trung tâm của mặt hàng số.
• Chú ý rằng, tùy nằm trong vô mặt hàng số của công ty đem tăng dần dần hoặc hạn chế dần dần, cơ hội vận dụng công thức hoàn toàn có thể thay cho thay đổi. Đối với mặt hàng số hạn chế dần dần, bạn cũng có thể cần thiết hòn đảo ngược phương pháp tính số hạng đầu và cuối Khi dùng công thức.

Với những Note này, các bạn sẽ thoải mái tự tin rộng lớn trong những công việc giải quyết và xử lý những vấn đề tính tổng mặt hàng số và vận dụng những công thức một cơ hội đúng mực. Chúc chúng ta trở thành công!

Công thức tính tổng mặt hàng số ko cơ hội đều

Khi chúng ta đương đầu với mặt hàng số ko cơ hội đều, như mặt hàng số Fibonacci hoặc những mặt hàng số đem quy tắc riêng rẽ, việc dò la công thức tổng hoàn toàn có thể trở thành thú vị và thỉnh thoảng phức tạp.

Ví dụ: Tính tổng mặt hàng số ko cơ hội đều

Xét bài xích toán: Tính A = 1 x 2 + 2 x 3 + 3 x 4 +…+ n x (n + 1).

Lời Giải:

Chúng tao tiếp tục sử dụng một cách thức quan trọng đặc biệt nhằm giải quyết và xử lý yếu tố này. Trước hết, tao nhân cả mặt hàng số với 3:

3 x A = 1 x 2 x 3 + 2 x 3 x 3 + 3 x 4 x 3 +…+ n x (n + 1) x 3

Khi không ngừng mở rộng và bố trí lại những số hạng, tao có:

3 x A = 1 x 2 x (3 – 0) + 2 x 3 x (4 – 1) + 3 x 4 x (5 – 2) +…+ n x (n + 1) x [(n + 2) – (n – 1)]

Dãy số này được bố trí lại thành:

3 x A = 1 x 2 x 3 + 2 x 3 x 4 – 1 x 2 x 3 + 3 x 4 x 5 – 2 x 3 x 4 +…+ n x (n + 1) x (n + 2) – (n – 1) x n x (n + 1)

Xem thêm: tính từ trong tiếng anh là gì

Khi chúng ta kiểm tra kỹ lưỡng, các bạn sẽ thấy rằng một vài số hạng có khả năng sẽ bị diệt vứt cho nhau. Kết trái khoáy ở đầu cuối tiếp tục chỉ từ lại:

3 x A = n x (n + 1) x (n + 2)

Và ở đầu cuối, phân chia cả nhị mặt mũi mang đến 3 nhằm dò la A:

A = n x (n + 1) x (n + 2) / 3

Một số vấn đề tính tổng mặt hàng số ko cơ hội đều và cơ hội đều

Sau Khi dò la làm rõ rộng lớn về công thức tính tổng mặt hàng số cơ hội đều và ko cơ hội đều, chúng ta nên xem thêm những bài xích tập dượt bên dưới nhằm vận dụng công thức hiệu suất cao hơn:

Bài thói quen tổng mặt hàng số cơ hội đều

Khi chúng ta thực hiện bài xích thói quen tổng mặt hàng số cơ hội đều, một vài ví dụ ví dụ tại đây tiếp tục khiến cho bạn làm rõ rộng lớn cơ hội tiếp cận và giải quyết:

Bài tập dượt 1: Tính độ quý hiếm của T với T = 2 + 3 + 4 + 5 +…+ 2015

Lời giải:

Tính số số hạng: Số số hạng vô mặt hàng là (2015 – 2) / 1 + 1 = năm trước.

Tính tổng: T = (2015 + 2) x năm trước / 2 = 2,030,042.

Đáp số: 2,030,042

Bài tập dượt 2: Tính tổng 40 số lẻ thường xuyên, biết số lẻ lớn số 1 là 2011.

Lời giải:

Tìm số lẻ nhỏ nhất: Số lẻ nhỏ nhất là 2011 – (40 – 1) x 2 = 1933.

Tính tổng: Tổng của 40 số lẻ = (2011 + 1933) x 40 / 2 = 78,880.

Đáp số: 78,880

Bài tập dượt 3: Một thành phố đem 25 căn nhà với số căn nhà là những số lẻ thường xuyên, tổng số căn nhà là 1145. Hỏi số căn nhà trước tiên là bao nhiêu?

Lời giải:

Tính khoảng cộng: Trung bình nằm trong của mặt hàng số là 1145 / 25 = 45,8.

Tìm số căn nhà đầu tiên: Số căn nhà trước tiên = 45,8 – (25 – 1) x 2 / 2 = 9.

Đáp số: 9

Lưu ý:

• Sử dụng công thức tính tổng mặt hàng số cơ hội đều: T = (Số Hạng Đầu + Số Hạng Cuối) x Số Số Hạng / 2.
• Luôn đánh giá kỹ số hạng đầu và cuối rưa rứa con số số hạng vô mặt hàng.
• Hãy demo thực hiện thêm thắt nhiều bài xích tập dượt không giống nhau nhằm nắm rõ cơ hội dùng công thức.

Bài thói quen tổng mặt hàng số ko cơ hội đều

Bên cạnh những bài xích tập dượt tương quan cho tới công thức tính tổng mặt hàng số cơ hội đều, bên dưới đó là một vài bài xích tập dượt nhằm luyện công thức tính tổng mặt hàng số ko cơ hội đều nhưng mà bạn cũng có thể tham ô khảo:

Bài Tập 1: Tính M = 1 x 2 x 3 + 2 x 3 x 4 +…+ (n – 1) x n x (n + 1).

Lời giải:

Nhân M với 4 và bố trí lại:

4 x M = 1 x 2 x 3 x 4 + 2 x 3 x 4 x 5 +…+ (n – 1) x n x (n + 1) x (n + 2) – (n – 2) x (n – 1) x n x (n + 1).

Kết quả:

M = [(n – 1) x n x (n + 1) x (n + 2)] / 4.

Đáp số: M = (n – 1) x n x (n + 1) x (n + 2) / 4

Bài Tập 2: Tính N = 1 x 4 + 2 x 5 + 3 x 6 + 4 x 7 +…+ n x (n + 3).

Lời giải:

Biến thay đổi từng số hạng:

N = 1 x 2 + 2 x 3 + 3 x 4 +…+ n x (n + 1) + (2 + 4 + 6 +…+ 2n).

Tính tổng mặt hàng số:

N = n(n + 1)(n + 2)/3 + (2n + 2)n/2.

Kết trái khoáy cuối cùng:

N = n(n + 1)(n + 5)/3.

Đáp số: N = n(n + 1)(n + 5)/3

Xem thêm: đạo hàm của căn x

Lưu ý:

• Việc thay đổi và bố trí lại những số hạng vô mặt hàng số là khóa xe nhằm dò la ra sức thức tổng.
• Hãy chắc hẳn rằng rằng từng bước thay đổi được triển khai một cơ hội đúng mực.
• Càng thực hành thực tế nhiều, chúng ta càng đơn giản và dễ dàng nhìn thấy kiểu số trong số mặt hàng số và vận dụng công thức một cơ hội linh động.

Tạm kết

Kết luận về nội dung bài viết công thức tính tổng mặt hàng số cơ hội đều, tất cả chúng ta hoàn toàn có thể thấy rằng việc hiểu và vận dụng công thức này là cực kỳ cần thiết trong những công việc giải quyết và xử lý nhiều loại vấn đề toán học tập. Công thức này không những giản dị và dễ dàng nắm bắt mà còn phải cực kỳ hữu ích trong những công việc tiết kiệm chi phí thời hạn và công sức của con người Khi tính tổng một mặt hàng số rộng lớn. Hình như, nội dung bài viết cũng cung ứng những ví dụ ví dụ và lời nói giải cụ thể, hùn người chúng ta đơn giản và dễ dàng hiểu và vận dụng công thức vô thực tiễn.

Xem thêm:

• Bộ công thức Hoán vị – Chỉnh thích hợp – Tổ thích hợp rất đầy đủ nhất vô Toán học
• Công thức tính thể tích hình cầu và diện tích S hình cầu