cho hình chóp sabcd có đáy abcd là hình vuông cạnh a

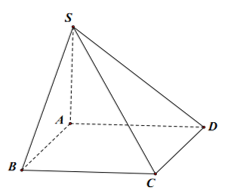
Hình chóp S.ABCD đem lòng là hình vuông vắn cạnh a, SA vuông góc với lòng và SA = a. Góc thân thích nhì mặt mày bằng phẳng (SAB) và (SCD) bằng?

Góc thân thích nhì mặt mày bằng phẳng (SAB) và (SCD) rất có thể mò mẫm bằng phương pháp dùng công thức tính góc thân thích nhì mặt mày bằng phẳng.
Công thức tính góc thân thích nhì mặt mày bằng phẳng là:
cos(θ) = (n₁ · n₂) / (||n₁|| · ||n₂||)
Trong tê liệt, n₁ và n₂ là nhì vector pháp tuyến của nhì mặt mày bằng phẳng ứng và ||n₁|| và ||n₂|| là chừng lâu năm của bọn chúng.
Trong tình huống này, mặt mày bằng phẳng (SAB) đem vector pháp tuyến là AB và mặt mày bằng phẳng (SCD) đem vector pháp tuyến là CD.
Do lòng là hình vuông vắn ABCD, nên vector pháp tuyến AB và CD đều vuông góc với lòng và nằm trong chiều với SA.
Vì vậy, nhằm tính góc thân thích nhì mặt mày bằng phẳng (SAB) và (SCD), tất cả chúng ta chỉ việc tính góc thân thích nhì vector pháp tuyến AB và CD.
Ta có:
cos(θ) = (AB · CD) / (||AB|| · ||CD||)
Do lòng là hình vuông vắn cạnh a, nên chừng lâu năm của nhì vector pháp tuyến AB và CD đều vì chưng a.
Vậy công thức tính góc thân thích nhì mặt mày bằng phẳng (SAB) và (SCD) là:
cos(θ) = (AB · CD) / (a · a)
Để mò mẫm góc θ, tất cả chúng ta rất có thể dùng hình học tập hoặc những cách thức đo lường và tính toán không giống nhằm tính cos(θ) và tiếp sau đó tính arccos của độ quý hiếm này.

Để tính thể tích của hình chóp S.ABCD, tất cả chúng ta cần phải biết cạnh lòng và chừng lâu năm cạnh lòng vuông góc với cạnh lòng.
Với hình chóp S.ABCD đem lòng là hình vuông vắn cạnh a, tao đem biết SA là cạnh đứng vuông góc với lòng và đem chiều lâu năm vì chưng a.
Bước 1: Tìm diện tích S lòng của hình chóp:
Vì lòng là hình vuông vắn cạnh a, diện tích S lòng vì chưng a^2.
Bước 2: Tìm độ cao của hình chóp:
Do SA vuông góc với lòng, tao rất có thể tính độ cao SĂ của tam giác SAB bằng phương pháp dùng lăm le lý Pythagoras:
SĂ^2 = SB^2 - BA^2
SĂ^2 = a^2 - (a/2)^2
SĂ^2 = a^2 - a^2/4
SĂ^2 = 3a^2/4
SĂ = √(3a^2/4)
SĂ = √3a/2
Bước 3: Tính thể tích của hình chóp:
Công thức tính thể tích của hình chóp là:
Thể tích = (diện tích lòng x chiều cao)/3
Thể tích = (a^2 x √3a/2)/3
Thể tích = √3a^3/6
Vậy, thể tích của hình chóp S.ABCD là √3a^3/6.

Để mò mẫm khoảng cách kể từ điểm A cho tới mặt mày bằng phẳng lòng của hình chóp S.ABCD, tao rất có thể dùng công thức tỉ trọng Pytago.
Giả sử điểm M là trung điểm của cạnh AB, tao đem AM = MB = a/2 (do ABCD là hình vuông).
Xét tam giác vuông AMB, tao đem AM^2 + MB^2 = AB^2.
Thay nhập độ quý hiếm tiếp tục biết, tao đem (a/2)^2 + (a/2)^2 = a^2.
Từ tê liệt, tao suy rời khỏi a^2/4 + a^2/4 = a^2.
Simplificar phương trình, tao đem a^2/2 = a^2.
Lấy căn both phía nhì vế, tao được căn nhì a^2/2 = căn nhì a^2.
Tức là a / căn nhì 2 = a
Vậy, khoảng cách kể từ điểm A cho tới mặt mày bằng phẳng lòng của hình chóp S.ABCD là a.

Để tính chừng lâu năm cạnh SC của hình chóp S.ABCD, tao cần dùng những vấn đề tiếp tục cho:
- Đáy của hình chóp là hình vuông vắn cạnh a.
- Cạnh SA của hình chóp là đoạn trực tiếp vuông góc với lòng và có tính lâu năm là a.
Ta rất có thể dùng lăm le lý Pythagoras nhằm tính chừng lâu năm cạnh SC. bằng phẳng việc đánh giá tam giác SCA, tao thấy:
SC^2 = SA^2 + AC^2
Vì lòng ABCD là hình vuông vắn cạnh a, nên cạnh AC cũng có thể có chừng lâu năm a. Thay nhập công thức bên trên, tao có:
SC^2 = a^2 + a^2
SC^2 = 2a^2
Do đó:
SC = √(2a^2)
SC = √2 * a
Vậy chừng lâu năm cạnh SC là √2 * a.

Để tính tổng chừng lâu năm những cạnh ở mặt mày mặt của hình chóp S.ABCD, tất cả chúng ta cần phải biết chừng lâu năm của những cạnh độc nhất của hình chóp.
Vì lòng là một trong hình vuông vắn cạnh a, tao đem 4 cạnh trong tâm thức là AB, BC, CD và DA. Vì đó là hình vuông vắn nên chừng lâu năm những cạnh này đều vì chưng a.
Tiếp theo đòi, tao cần thiết tính chừng lâu năm của cạnh SA, góc thân thích nhì mặt mày bằng phẳng (SAB) và (SCD).
Thông tin cẩn nhập thắc mắc cho thấy thêm SA vuông góc với lòng và SA = a. Như vậy Tức là SA là một trong cạnh của hình chóp, có tính lâu năm a.
Khi tiếp tục biết chừng lâu năm của những cạnh độc nhất của hình chóp, tao cần thiết tính tổng chừng lâu năm những cạnh ở mặt mày mặt của hình chóp.
Tổng chừng lâu năm những cạnh ở mặt mày mặt của hình chóp vì chưng tổng của những cạnh lòng và cạnh đứng (SA).
Do lòng là một trong hình vuông vắn cạnh a, nên tổng chừng lâu năm những cạnh lòng vì chưng 4a.
Tổng chừng lâu năm những cạnh ở mặt mày mặt của hình chóp là 4a + a = 5a.
Vậy, tổng chừng lâu năm những cạnh ở mặt mày mặt của hình chóp S.ABCD là 5a.

Để mò mẫm góc thân thích đường thẳng liền mạch SA và mặt mày bằng phẳng lòng ABCD, tao cần thiết mò mẫm góc thân thích đường thẳng liền mạch SA và một đường thẳng liền mạch phía trên mặt mày bằng phẳng lòng.
Vì SA vuông góc với lòng ABCD, tao rất có thể lựa chọn 1 đường thẳng liền mạch SB phía trên mặt mày bằng phẳng lòng ABCD sao cho tới SB tuy vậy song với SA.
Giả sử SB và SA là nhì cạnh không giống nhau của lòng ABCD. Khi tê liệt, nhập tam giác SAB, tao mang 1 cặp cạnh vuông góc cùng nhau (SA vuông góc với AB).
Do tê liệt, góc thân thích đường thẳng liền mạch SA và mặt mày bằng phẳng lòng ABCD đó là góc thân thích đường thẳng liền mạch SA và đường thẳng liền mạch SB.
Vì SB tuy vậy song với SA, nên góc thân thích SA và SB đó là góc thân thích đường thẳng liền mạch SA và mặt mày bằng phẳng lòng ABCD.
Từ tê liệt, tao rất có thể dùng kiến thức và kỹ năng về hình học tập nhằm tính góc thân thích SA và SB.

Để tính diện tích S mặt mày bằng phẳng SCD nhập hình chóp S.ABCD, tao dùng công thức diện tích S một tam giác:
Diện tích tam giác SCD = một nửa * cạnh AB * cạnh SD * sin(góc thân thích nhì cạnh)
Trong tê liệt, cạnh AB là cạnh của lòng hình vuông vắn (cạnh a), cạnh SD là cạnh của hình chóp (cạnh SA), và góc thân thích nhì cạnh là góc thân thích nhì mặt mày bằng phẳng (SAB) và (SCD).
Vì SA vuông góc với lòng và SA = a, nên cạnh SD tiếp tục cũng vì chưng a.
Góc thân thích nhì mặt mày bằng phẳng (SAB) và (SCD) rất có thể tính được vì chưng công thức:
sin(góc thân thích nhì mặt mày phẳng) = SA/SD
Với SA = a và SD = a, tao có:
sin(góc thân thích nhì mặt mày phẳng) = a/a = 1
Do tê liệt, góc thân thích nhì mặt mày bằng phẳng (SAB) và (SCD) vì chưng 90 chừng.
Tiếp theo đòi, tao tính diện tích S mặt mày bằng phẳng SCD:
Diện tích tam giác SCD = một nửa * a * a * sin(90°) = một nửa * a * a * 1 = một nửa * a^2
Vậy, diện tích S mặt mày bằng phẳng SCD của hình chóp S.ABCD là một nửa * a^2.

Để tính diện tích S toàn phần của hình chóp S.ABCD, tao cần thiết tính diện tích S những mặt mày mặt và diện tích S lòng của hình chóp.
Bước 1: Tính diện tích S những mặt mày mặt của hình chóp.
Vì SA vuông góc với lòng và lòng là hình vuông vắn cạnh a, nên tao đem những cạnh lòng là AB = BC = CD = AD = a.
Đặt AC = d là độ cao của tam giác vuông SAB và SCD.
Theo khái niệm, diện tích S tam giác vuông SAB và SCD theo đòi công thức là:
S(SAB) = (1/2) * AB * AC = (1/2) * a * d
S(SCD) = (1/2) * CD * AC = (1/2) * a * d
Do tê liệt, diện tích S từng mặt mày mặt của hình chóp là S(SAB) và S(SCD).
Bước 2: Tính diện tích S lòng của hình chóp.
Đáy của hình chóp là hình vuông vắn đem cạnh a, nên diện tích S lòng là S(ABCD) = a * a.
Bước 3: Tính diện tích S toàn phần của hình chóp.
Diện tích toàn phần của hình chóp được xem vì chưng tổng diện tích S những mặt mày mặt và diện tích S lòng.
S(toàn phần) = S(SAB) + S(SCD) + S(ABCD) = (1/2) * a * d + (1/2) * a * d + a * a = a * d + a * d + a * a = 2ad + a^2.
Vậy, diện tích S toàn phần của hình chóp S.ABCD là 2ad + a^2.

Để mò mẫm chừng lâu năm đàng vội vàng khúc kể từ B cho tới mặt mày bằng phẳng SCD, tất cả chúng ta cần thiết mò mẫm lối đi kể từ B cho tới mặt mày bằng phẳng SCD sao cho tới phía trên mặt mày bằng phẳng vuông góc với đường thẳng liền mạch AB và trải qua điểm C. Các bước triển khai như sau:
Bước 1: Vẽ hình vẽ cho tới việc như nhập câu hỏi: hình chóp S.ABCD đem lòng là hình vuông vắn cạnh a, và SA vuông góc với lòng.
Bước 2: Xác lăm le những vấn đề tiếp tục cho tới và những vấn đề cần thiết mò mẫm. Ta được cho tới chừng lâu năm cạnh AB của hình vuông vắn ABCD là a. Ta cần thiết mò mẫm chừng lâu năm đàng vội vàng khúc kể từ B cho tới mặt mày bằng phẳng SCD.
Bước 3: Gọi I là phó điểm của đường thẳng liền mạch AB và mặt mày bằng phẳng SCD. Ta cần thiết mò mẫm chừng lâu năm lối đi kể từ B cho tới I.
Bước 4: Ta hiểu được SA vuông góc với lòng ABCD nên tao đem AB ⊥ SA. Do tê liệt, I là hình chiếu vuông góc của B lên đường thẳng liền mạch SA.
Bước 5: Kéo dựng lối đi vội vàng khúc kể từ B cho tới I, và kẻ đường thẳng liền mạch CI.
Bước 6: Ta rất có thể nhận biết tứ giác SCI là tứ giác đều, vì như thế đó là một hình chóp đều. Vì lòng ABCD là hình vuông vắn cạnh a, nên SC = CD = a. Do tê liệt, SC = CI = a.
Bước 7: kề dụng lăm le lí Pythagoras, tao có: BC² = CI² + IB². Vì SC = CI = a và IB = AB = a, nên tao đem BC² = a² + a² = 2a².
Bước 8: Từ tê liệt, tao suy rời khỏi BC = √(2a²) = √2 * a.
Vậy, chừng lâu năm đàng vội vàng khúc kể từ B cho tới mặt mày bằng phẳng SCD là √2 * a.