Chủ đề Cách tính diện tích S chu vi hình vuông: Cách tính diện tích S và chu vi hình vuông vắn đặc biệt đơn giản và giản dị và tiện nghi. Đối với hình vuông vắn, diện tích S đó là cạchnh nhân với chủ yếu nó, trong lúc cơ chu vi là tổng phỏng nhiều năm của tứ cạnh. Từ công thức đơn giản và giản dị này, tao rất có thể nhanh gọn lẹ đo lường và phần mềm nhập những câu hỏi thực tiễn. Việc này hùn tất cả chúng ta thâu tóm được vấn đề cần thiết và tăng kĩ năng xử lý những yếu tố tương quan cho tới hình vuông vắn.
Cách tính diện tích S của hình vuông?
Cách tính diện tích S của hình vuông vắn đặc biệt đơn giản và giản dị. quý khách hàng chỉ việc tuân theo công việc sau:
1. Xác quyết định chiều nhiều năm cạnh hình vuông: Để tính diện tích S của hình vuông vắn, trước tiên, các bạn nên biết chiều nhiều năm của từng cạnh. Gọi cạnh hình vuông vắn là \"a\".
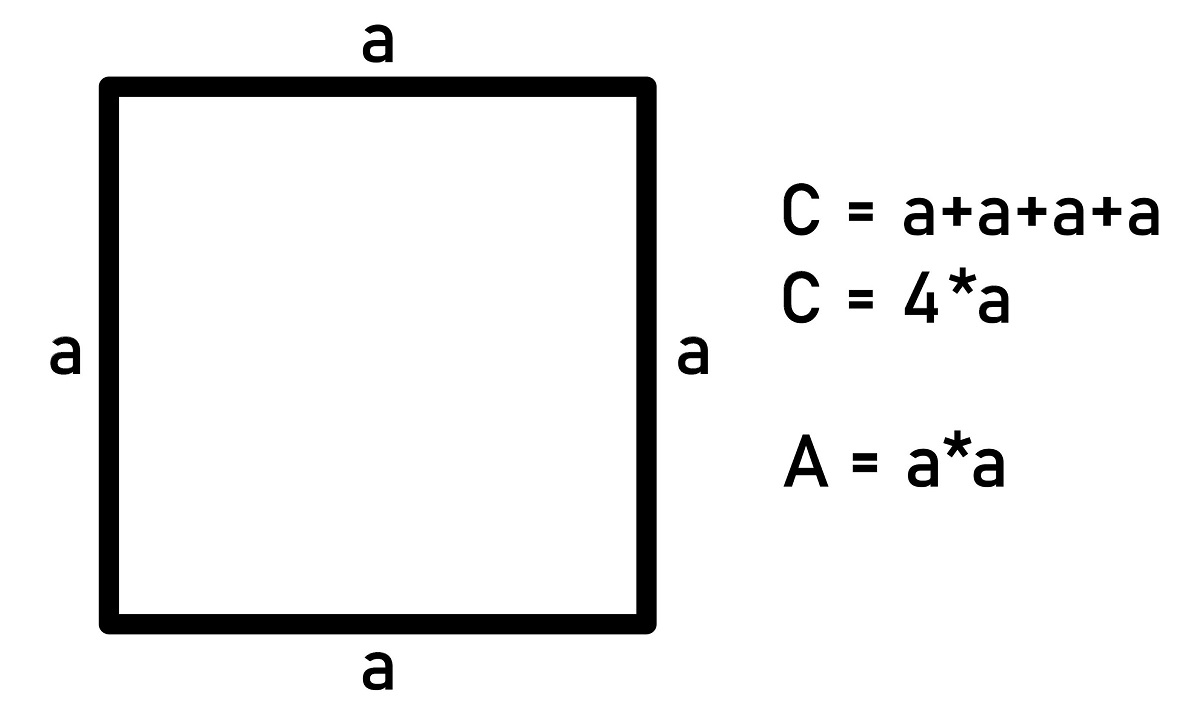
2. Sử dụng công thức: Diện tích của hình vuông vắn được xem bằng phương pháp nhân chiều nhiều năm cạnh với chủ yếu nó. Vậy công thức nhằm tính diện tích S của hình vuông vắn là: S = a x a hoặc S = a^2. (Trong cơ, \"S\" là ký hiệu của diện tích S và \"a\" là chiều nhiều năm cạnh hình vuông).
Ví dụ: Nếu cạnh của hình vuông vắn là 5 centimet, tao rất có thể tính diện tích S bằng phương pháp nhân 5 centimet với chủ yếu nó: S = 5 centimet x 5 centimet = 25 cm^2. Vậy diện tích S của hình vuông vắn này là 25 cm^2.
Hy vọng rằng những vấn đề bên trên vẫn giúp cho bạn hiểu phương pháp tính diện tích S của hình vuông vắn.
Bạn đang xem: diện tích hình vuông lớp 3

Chu vi hình vuông vắn được xem vì chưng công thức nào?
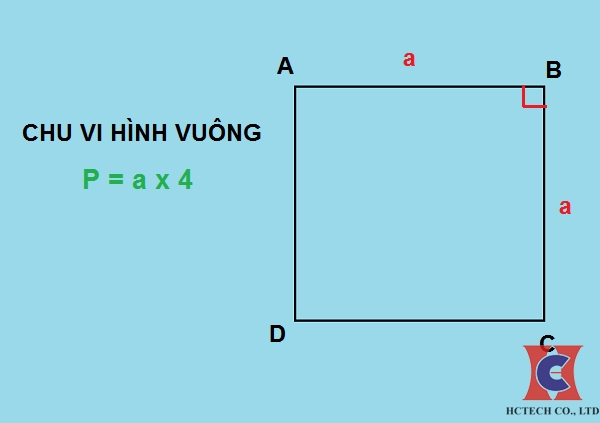
Chu vi hình vuông vắn được xem vì chưng công thức P.. = a x 4, nhập cơ a là phỏng nhiều năm của từng cạnh hình vuông vắn. Để tính chu vi hình vuông vắn, các bạn nên biết phỏng nhiều năm của từng cạnh. Sau cơ, nhân phỏng nhiều năm của từng cạnh với số 4 nhằm tính tổng phỏng nhiều năm của toàn bộ những cạnh.
Diện tích hình vuông vắn được xem vì chưng công thức nào?
Công thức tính diện tích S hình vuông vắn là bình phương của phỏng nhiều năm cạnh. Để tính diện tích S hình vuông vắn, tao dùng công thức: S = a^2. Trong số đó, S là diện tích S, và a là phỏng nhiều năm cạnh của hình vuông vắn.

Cho ví dụ rõ ràng về kiểu cách tính chu vi hình vuông vắn.
Để tính chu vi của một hình vuông vắn, tất cả chúng ta rất có thể dùng công thức P.. = a x 4, nhập cơ P.. là chu vi hình vuông vắn, và a là phỏng nhiều năm của một cạnh của hình vuông vắn cơ.
Ví dụ, fake sử tất cả chúng ta với cùng 1 hình vuông vắn có tính nhiều năm cạnh là 5 centimet. Ta rất có thể tính chu vi bằng phương pháp nhân phỏng nhiều năm cạnh này với 4:
P = 5 centimet x 4 = trăng tròn cm
Vậy chu vi của hình vuông vắn này là trăng tròn centimet.
Hy vọng phần vấn đáp này rất có thể giúp cho bạn hiểu phương pháp tính chu vi của một hình vuông vắn.
Cho ví dụ rõ ràng về kiểu cách tính diện tích S hình vuông vắn.
Để tính diện tích S của một hình vuông vắn, tao rất có thể dùng công thức đơn giản: diện tích S = cạnh x cạnh. Ví dụ, fake sử tất cả chúng ta với cùng 1 hình vuông vắn với cạnh có tính nhiều năm 5 centimet.
Để tính diện tích S của hình vuông vắn này, tất cả chúng ta thay cho độ quý hiếm cạnh nhập công thức diện tích S = cạnh x cạnh, tao có:
Diện tích = 5 centimet x 5 centimet = 25 cm².
Vậy diện tích S của hình vuông vắn này là 25 cm².
Xem thêm: ngày xuân con én đưa thoi
_HOOK_
Công thức tính diện tích S và chu vi hình vuông
Học tính diện tích S và chu vi hình vuông vắn đơn giản và dễ dàng với công thức đơn giản và giản dị. Xem đoạn phim nhằm nắm rõ phương pháp tính và phần mềm vô nằm trong hữu ích của công thức này nhập thực tiễn. Đừng bỏ dở, hãy coi ngay!
Công thức tính chu vi và diện tích S hình vuông vắn Toán kể từ lớp 2 đi học 5
Muốn thám thính hiểu về kiểu cách tính chu vi và diện tích S hình vuông vắn sao mang lại chủ yếu xác? Video này cung ứng cho chính mình từng vấn đề quan trọng, kể từ công thức cho tới ví dụ minh họa. Khám huỷ tức thì nhằm phát triển thành Chuyên Viên về hình vuông!
Làm thế nào là để tìm hiểu chiều nhiều năm của những cạnh hình vuông?
Để biết chiều nhiều năm của những cạnh hình vuông vắn, chúng ta có thể vận dụng công việc sau đây:
Bước 1: Xác quyết định vấn đề với sẵn
Nếu nhập câu hỏi vẫn cung ứng cho chính mình những vấn đề như chu vi (P) hoặc diện tích S (S) của hình vuông vắn, chúng ta có thể dùng những công thức ứng nhằm đo lường chiều nhiều năm cạnh.
Bước 2: Sử dụng công thức tính chu vi (P)
Chu vi của hình vuông vắn vì chưng tích cạnh (a) nhân 4, tức là P.. = a x 4. Do cơ, nếu khách hàng vẫn biết chu vi (P) của hình vuông vắn, chúng ta có thể tính được chiều nhiều năm cạnh (a) bằng phương pháp phân tách P.. mang lại 4.
Bước 3: Sử dụng công thức tính diện tích S (S)
Diện tích của hình vuông vắn vì chưng bình phương cạnh (a) hoặc vì chưng tích nhì cạnh như nhau (a x a). Nếu các bạn vẫn biết diện tích S (S) của hình vuông vắn, chúng ta có thể tính được chiều nhiều năm cạnh (a) vì chưng căn bậc nhì của diện tích S.
Ví dụ:
Nếu nhập câu hỏi cung ứng cho chính mình chu vi (P) là 12, chúng ta có thể dùng công thức P.. = a x 4 nhằm tính chiều nhiều năm cạnh như sau:
12 = a x 4
a = 12 / 4
a = 3
Tương tự động, nếu như nhập câu hỏi cung ứng diện tích S (S) là 9, chúng ta có thể dùng công thức S = a x a nhằm tính chiều nhiều năm cạnh như sau:
9 = a x a
a² = 9
a = √9
a = 3
Vậy chiều nhiều năm của những cạnh hình vuông vắn nhập ví dụ này là 3.
Làm thế nào là nhằm tính chu vi lúc biết diện tích S hình vuông?
Để tính chu vi của một hình vuông vắn lúc biết diện tích S, tao cần thiết vận dụng những công thức tương quan. Trước tiên, tao tiếp tục tính phỏng nhiều năm cạnh của hình vuông vắn vì chưng căn bậc nhì của diện tích S. Sau cơ, tao nhân cạnh với số 4 nhằm tính được chu vi.
Dưới đấy là tiến độ cụ thể nhằm tính chu vi lúc biết diện tích S của hình vuông:
1. Gọi S là diện tích S hình vuông vắn.
2. Tính phỏng nhiều năm cạnh vì chưng căn bậc nhì của diện tích S: a = √S.
3. Tính chu vi bằng phương pháp nhân cạnh với 4: P.. = a x 4.
Ví dụ, fake sử diện tích S hình vuông vắn là 16 đơn vị chức năng diện tích S (đơn vị dạng đơn vị chức năng đo diện tích S, ví dụ: cm²). sát dụng công thức trên:
1. Diện tích hình vuông vắn là S = 16 cm².
2. Tính phỏng nhiều năm cạnh vì chưng căn bậc nhì của diện tích S: a = √16 = 4 centimet.
3. Tính chu vi bằng phương pháp nhân cạnh với 4: P.. = 4 centimet x 4 = 16 centimet.
Do cơ, lúc biết diện tích S của hình vuông vắn là 16 cm², chu vi của hình vuông vắn là 16 centimet.
Lưu ý rằng Khi vận dụng công thức này, đại lượng diện tích S và chu vi nên với nằm trong đơn vị chức năng đo nhằm thành quả đo lường đúng đắn.
Làm thế nào là nhằm tính diện tích S lúc biết chu vi hình vuông?
Để tính diện tích S hình vuông vắn lúc biết chu vi, tao rất có thể dùng công thức sau:
1. Gọi a là phỏng nhiều năm một cạnh của hình vuông vắn.
2. Chu vi (P) của hình vuông vắn là tích đằm thắm phỏng nhiều năm một cạnh (a) và số 4 (P = a x 4).
3. Để tính diện tích S (S), tao sử dụng công thức S = a^2, nhập cơ a là phỏng nhiều năm một cạnh của hình vuông vắn.
Ví dụ: Giả sử chu vi hình vuông vắn là 24 centimet, tao rất có thể vận dụng công thức nhằm tính diện tích S như sau:
1. Gọi a là phỏng nhiều năm một cạnh của hình vuông vắn.
2. Chu vi của hình vuông vắn là 24 centimet, vậy tao với phương trình 24 = a x 4. Từ cơ, tao với a = 6 centimet.
3. Để tính diện tích S, tao sử dụng công thức S = a^2, nhập cơ a là phỏng nhiều năm một cạnh của hình vuông vắn. Vậy diện tích S của hình vuông vắn là S = 6^2 = 36 cm^2.
Vậy lúc biết chu vi hình vuông vắn, tao rất có thể tính được diện tích S bằng phương pháp dùng công thức S = a^2, nhập cơ a là phỏng nhiều năm một cạnh của hình vuông vắn được xem vì chưng chu vi phân tách mang lại 4 (a = chu vi / 4).
Tại sao phương pháp tính diện tích S và chu vi hình vuông vắn lại khá đơn giản?
Cách tính diện tích S và chu vi của hình vuông vắn khá đơn giản và giản dị vì thế những đặc điểm của hình vuông vắn thực hiện mang lại quy trình đo lường trở thành đơn giản và dễ dàng. Dưới đấy là nguyên do bên trên sao:
1. Chu vi hình vuông: Chu vi của hình vuông vắn được xem vì chưng công thức P.. = a x 4, nhập cơ a là phỏng nhiều năm cạnh của hình vuông vắn. Vì hình vuông vắn với 4 cạnh đều bằng nhau, cho nên việc tính chu vi trở thành đơn giản và giản dị rộng lớn. Ta chỉ việc nhân phỏng nhiều năm cạnh với số 4 để sở hữu được chu vi của hình vuông vắn. Ví dụ, nếu như cạnh hình vuông vắn là 5 centimet, thì chu vi được xem là 5 centimet x 4 = trăng tròn centimet.
2. Diện tích hình vuông: Diện tích của hình vuông vắn được xem vì chưng công thức S = a^2, nhập cơ a là phỏng nhiều năm cạnh của hình vuông vắn. Vì toàn bộ những cạnh của hình vuông vắn đều bằng nhau, tao chỉ việc bình phương phỏng nhiều năm cạnh nhằm tính diện tích S. Ví dụ, nếu như cạnh hình vuông vắn là 5 centimet, thì diện tích S được xem là 5 cm^2 = 25 cm^2.
3. Tính hóa học đối xứng: Hình vuông với đặc điểm đối xứng, tức là nếu như tất cả chúng ta biết chiều nhiều năm của một cạnh, tao cũng hiểu rằng chiều nhiều năm của toàn bộ những cạnh không giống. Vấn đề này thực hiện mang lại việc tính diện tích S và chu vi của hình vuông vắn trở thành đơn giản và giản dị rộng lớn đối với những hình dạng khác ví như hình chữ nhật hoặc hình tam giác.
Tóm lại, phương pháp tính diện tích S và chu vi của hình vuông vắn đơn giản và giản dị nhờ đặc điểm cơ bạn dạng của hình vuông vắn và đặc điểm đối xứng của chính nó. Việc chỉ nên biết phỏng nhiều năm cạnh nhằm đo lường thực hiện mang lại quy trình này trở thành nhanh gọn lẹ và thuận tiện.
Xem thêm: chuỗi truyền electron tạo ra
Có những phần mềm nào là của việc tính diện tích S và chu vi hình vuông vắn nhập thực tế?
Có nhiều phần mềm của việc tính diện tích S và chu vi hình vuông vắn nhập thực tiễn. Dưới đấy là một số trong những phần mềm phổ biến:
1. Xây dựng và thi đua công: Khi design và xây cất những công trình xây dựng như nhà tại, cầu đường giao thông, hoặc điểm xanh rớt công nằm trong, việc đo lường diện tích S và chu vi hình vuông vắn là đặc biệt cần thiết. Giúp xác lập con số vật tư quan trọng như gạch ốp, mộc, xi-măng, cỏ tự tạo, viền đá cảnh, và tổng ngân sách mang lại việc xây cất.
2. Kinh doanh không cử động sản: Đối với môi giới nhà đất, tính diện tích S và chu vi hình vuông vắn của 1 căn ngôi nhà hoặc một khu đất nền đặc biệt quan trọng nhằm xác lập độ quý hiếm tòa nhà hoặc độ quý hiếm thương nghiệp của khu đất nền. Người mua sắm và góp vốn đầu tư rất có thể dùng vấn đề này để lấy đi ra ra quyết định giao thương hoặc góp vốn đầu tư.
3. Tính diện tích S khu đất nông nghiệp: Khi thao tác nhập nghành nghề dịch vụ nông nghiệp, tính diện tích S hình vuông vắn của một mảnh đất nền nông nghiệp đặc biệt cần thiết nhằm đo lường con số cây cỏ, lượng phân bón và quy hướng việc trồng trọt.
4. Thiết tiếp không khí nội thất: Trong nghành nghề dịch vụ design thiết kế bên trong, tính diện tích S và chu vi hình vuông vắn hùn xác lập độ dài rộng và kiểu dáng của những đồ vật thiết kế bên trong như bàn và ghế, kệ tủ, chóng và hành lang cửa số. Vấn đề này hùn đáp ứng phù phù hợp với không khí và tạo ra sự bằng phẳng mang lại không khí sinh sống.
5. Tính diện tích S và chu vi khu đất phân lô: Khi mua mảnh đất và phân lô nhằm xây nhà ở riêng biệt, tính diện tích S và chu vi hình vuông vắn là đặc biệt cần thiết nhằm đo lường điểm khu đất, phân loại mặt phẳng, và xây cất theo gót quy quyết định của sổ đỏ chính chủ.
6. Hiểu về quy tế bào ko gian: Tính diện tích S và chu vi hình vuông vắn hùn tất cả chúng ta tưởng tượng và hiểu về quy tế bào không khí xung xung quanh. Ví dụ, Khi tính diện tích S và chu vi hình vuông vắn của một khu vui chơi công viên hay như là một điểm giảng lối, tất cả chúng ta rất có thể Đánh Giá được tổng quan liêu về độ dài rộng và quy tế bào của vị trí cơ.
Trên đấy là một số trong những phần mềm thực tiễn của việc tính diện tích S và chu vi hình vuông vắn. Việc vận dụng công thức tính diện tích S và chu vi hình vuông vắn nhập những trường hợp nhập cuộc sống đời thường từng ngày đặc biệt hữu ích và quan trọng.
_HOOK_










Bình luận