góc giữa 2 đường thẳng trong không gian

Cách tính góc thân mật hai tuyến phố trực tiếp nhập không khí là gì?

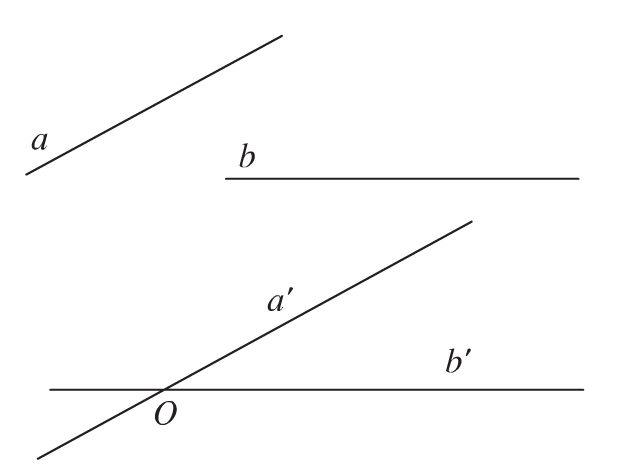
Góc thân mật hai tuyến phố trực tiếp nhập không khí là góc thân mật hai tuyến phố trực tiếp nằm trong trải qua một điểm và theo lần lượt tuy vậy song với hai tuyến phố trực tiếp cơ. Để tính góc thân mật hai tuyến phố trực tiếp nhập không khí, tao nên nhớ công thức sau:
1. Tìm góc thân mật nhì đoạn thẳng: Để tính góc thân mật nhì đoạn trực tiếp AB và CD, tao dùng công thức sau:
cos θ = (AB • CD) / (|AB| • |CD|)
Trong cơ, AB • CD là tích vô vị trí hướng của nhì vector AB và CD, và |AB| • |CD| là tích chừng nhiều năm của nhì vector AB và CD.
2. Tính góc thân mật hai tuyến phố thẳng: Để tính góc thân mật hai tuyến phố trực tiếp AB và CD, tao dùng công thức:
θ = arccos (cos θ)
Trong cơ, cos θ là cosin của góc thân mật nhì đoạn trực tiếp AB và CD, và arccos là hàm arc cosin nhằm tính góc kể từ cosin.
Tóm lại, nhằm tính góc thân mật hai tuyến phố trực tiếp nhập không khí, tao cần thiết mò mẫm góc thân mật nhì đoạn trực tiếp dựa vào công thức tính cosin và tiếp sau đó dùng hàm arccos nhằm tính góc kể từ cosin.

Có tổng số 4 địa điểm kha khá thân mật hai tuyến phố trực tiếp nhập không khí.
1. Hai đường thẳng liền mạch hoàn toàn có thể rời nhau, tức là bọn chúng với cùng 1 điểm cộng đồng.
2. Hai đường thẳng liền mạch hoàn toàn có thể tuy vậy tuy vậy, tức là bọn chúng không tồn tại điểm cộng đồng và ko giao phó nhau.
3. Hai đường thẳng liền mạch cũng hoàn toàn có thể trùng nhau, tức là bọn chúng trọn vẹn trùng cùng nhau.
4. Hoặc hai tuyến phố trực tiếp hoàn toàn có thể chéo cánh nhau, tức là bọn chúng ko rời nhau và ko tuy vậy tuy vậy.

Nếu hai tuyến phố trực tiếp là tuy vậy song cùng nhau, thì góc thân mật bọn chúng là 0 chừng (hoặc 180 độ). Như vậy Có nghĩa là hai tuyến phố trực tiếp không tồn tại giao phó điểm và ko dẫn đến góc nào là. Hai đường thẳng liền mạch tuy vậy song với nằm trong phía, tức thị bọn chúng dịch rời theo đuổi và một phía và ko xa xôi nhau.
Để đánh giá coi hai tuyến phố trực tiếp với tuy vậy song hay là không, tao hoàn toàn có thể dùng cách thức đánh giá như sau:
- Xác lý thuyết của hai tuyến phố trực tiếp bằng phương pháp kiểm tra thông số góc (slope) của bọn chúng. Nếu hai tuyến phố trực tiếp với nằm trong thông số góc, tức là bọn chúng theo đuổi và một phía và là tuy vậy tuy vậy.
- Kiểm tra giao phó điểm của hai tuyến phố trực tiếp. Nếu bọn chúng không tồn tại nút giao, tức là bọn chúng là tuy vậy song cùng nhau.
Với những công thức và cách thức này, tất cả chúng ta hoàn toàn có thể xác lập được coi hai tuyến phố trực tiếp với tuy vậy song hay là không và tính góc thân mật bọn chúng nhập không khí.

Để tính góc thân mật hai tuyến phố trực tiếp Lúc bọn chúng rời nhau nhập không khí, tao hoàn toàn có thể triển khai công việc sau:
Bước 1: Xác toan điểm rời của hai tuyến phố trực tiếp. Điểm này là vấn đề nhưng mà hai tuyến phố trực tiếp rời nhau, và được gọi là vấn đề giao phó.
Bước 2: Xác toan nhì vector vị trí hướng của hai tuyến phố trực tiếp. Vector vị trí hướng của một đường thẳng liền mạch được xác lập bằng phương pháp lấy nhì điểm bên trên đường thẳng liền mạch và tính hiệu của bọn chúng. Trong tình huống hai tuyến phố trực tiếp rời nhau, tao lựa chọn nhì điểm bên trên hai tuyến phố trực tiếp không giống nhau và tính nhì vector phía ứng.
Bước 3: Tính tích vô vị trí hướng của nhì vector phía trải qua công thức tích vô hướng:
dot_product = vector_huong_1 * vector_huong_2 = |vector_huong_1| * |vector_huong_2| * cos(goc)
Trong cơ, |vector_huong_1| và |vector_huong_2| là chừng nhiều năm của nhì vector phía và cos(goc) là cosin của góc thân mật bọn chúng.
Bước 4: Tính góc thân mật hai tuyến phố trực tiếp trải qua công thức:
goc = arccos(dot_product / (|vector_huong_1| * |vector_huong_2|))
Bước 5: Đổi thành phẩm góc kể từ đơn vị chức năng radian quý phái đơn vị chức năng chừng nếu như quan trọng.
Ví dụ, nhằm tính góc thân mật đường thẳng liền mạch AB và đường thẳng liền mạch CD, tao triển khai công việc sau:
Bước 1: Tìm nút giao của đường thẳng liền mạch AB và đường thẳng liền mạch CD.
Bước 2: Xác toan nhì vector vị trí hướng của AB và CD.
Bước 3: Tính tích vô vị trí hướng của nhì vector hướng:
dot_product = vector_huong_AB * vector_huong_CD = |vector_huong_AB| * |vector_huong_CD| * cos(goc)
Bước 4: Tính góc thân mật hai tuyến phố thẳng:
goc = arccos(dot_product / (|vector_huong_AB| * |vector_huong_CD|))
Bước 5: Chuyển thay đổi thành phẩm góc kể từ radian quý phái chừng nếu như cần thiết.
Lưu ý: Khi tính góc thân mật hai tuyến phố trực tiếp, cần thiết để ý rằng công thức này chỉ vận dụng Lúc hai tuyến phố trực tiếp rời nhau. Trong tình huống hai tuyến phố trực tiếp tuy vậy song hoặc chéo cánh nhau, ko thể tính góc thân mật bọn chúng bằng phương pháp này.

Xem thêm: việc giải quyết vấn đề năng lượng ở bắc trung bộ chủ yếu dựa vào

Khi hai tuyến phố trực tiếp trùng nhau, góc thân mật bọn chúng được xem là 0 chừng. Như vậy Có nghĩa là hai tuyến phố trực tiếp trùng nhau ko dẫn đến góc rõ rệt. Khi hệt nhau như thế, không tồn tại góc thân mật hai tuyến phố trực tiếp được tạo hình và góc thân mật bọn chúng được xem là bởi vì 0 chừng.

Để tính góc thân mật hai tuyến phố trực tiếp chéo cánh nhau nhập không khí, tao hoàn toàn có thể tuân theo công việc sau đây:
Bước 1: Tìm nút giao của hai tuyến phố trực tiếp. Điểm này đó là điểm nhưng mà hai tuyến phố trực tiếp chéo cánh nhau rời nhau.
Bước 2: Xác toan nhì vector chỉ phương của hai tuyến phố trực tiếp. Vector chỉ phương đường thẳng liền mạch loại nhất (ví dụ A) hoàn toàn có thể được xác lập bằng phương pháp lấy nhì điểm phía trên đường thẳng liền mạch cơ (ví dụ A1 và A2) và tính vector AB = A2 - A1. Tương tự động, vector chỉ phương đường thẳng liền mạch loại nhì (ví dụ B) cũng khá được xác lập bằng phương pháp lấy nhì điểm phía trên đường thẳng liền mạch cơ (ví dụ B1 và B2) và tính vector BC = B2 - B1.
Bước 3: Tính tích vô vị trí hướng của nhì vector chỉ phương. Tích vô vị trí hướng của nhì vector chỉ phương A và B được xem bởi vì công thức AB * BC = |A| * |B| * cosθ, nhập cơ θ là góc thân mật hai tuyến phố trực tiếp.
Bước 4: Tính góc thân mật hai tuyến phố trực tiếp. Góc thân mật hai tuyến phố trực tiếp hoàn toàn có thể được xem bằng phương pháp dùng toan lý hàm số cosin nhập tam giác ABC: cosθ = (AB * BC) / (|A| * |B|). Sau cơ, vận dụng công thức arcsin(thetacos) nhằm tính góc θ.
Với công việc bên trên, tất cả chúng ta hoàn toàn có thể tính được góc thân mật hai tuyến phố trực tiếp chéo cánh nhau nhập không khí.

Công thức được dùng nhằm tính góc thân mật hai tuyến phố trực tiếp nhập không khí lúc biết những đường thẳng liền mạch tạo nên trở nên một tam giác là Định lý hàm số cosin nhập tam giác.
Để vận dụng công thức này, tao nên biết chừng nhiều năm những cạnh của tam giác được tạo nên trở nên bởi vì hai tuyến phố trực tiếp và đoạn trực tiếp nối những nút giao của hai tuyến phố trực tiếp cơ với đường thẳng liền mạch một.
Công thức Định lý hàm số cosin nhập tam giác là:
cosθ = (c² + a² - b²) / (2ac)
Trong đó:
- θ là góc thân mật hai tuyến phố trực tiếp nhập không khí.
- a, b, c là chừng nhiều năm tía cạnh của tam giác, với a là chừng nhiều năm đoạn trực tiếp nối những nút giao của hai tuyến phố trực tiếp, b và c là chừng nhiều năm đoạn trực tiếp thực hiện cạnh tam giác với a.
Sau Lúc có mức giá trị của cosθ, tao hoàn toàn có thể tính được góc θ bằng phương pháp dùng hàm ngược của hàm cos, tức là:
θ = arccos(cosθ)
Với những độ quý hiếm được xem toán, tao hoàn toàn có thể hiểu rằng góc thân mật hai tuyến phố trực tiếp nhập không khí.

Để tính được góc thân mật hai tuyến phố trực tiếp nhập không khí Lúc chỉ biết chừng nhiều năm những cạnh của tam giác tạo nên bởi vì hai tuyến phố trực tiếp và góc thân mật bọn chúng, tao hoàn toàn có thể dùng toan lý hàm số cosin nhập tam giác.
Bước 1: Tìm chừng nhiều năm những cạnh của tam giác
Đầu tiên, tao cần thiết xác lập những chừng nhiều năm của những cạnh của tam giác tạo nên bởi vì hai tuyến phố trực tiếp và góc thân mật bọn chúng. cũng có thể dùng toan lý Pythagoras hoặc công thức tính khoảng cách thân mật nhì điểm nhằm đo lường và tính toán chừng nhiều năm những cạnh.
Bước 2: sít dụng công thức cosin
Sau Lúc đang được biết chừng nhiều năm những cạnh của tam giác, tao hoàn toàn có thể vận dụng công thức cosin nhằm tính góc thân mật hai tuyến phố trực tiếp. Công thức nhằm tính góc thân mật hai tuyến phố trực tiếp nhập không khí là:
cosine(θ) = (a^2 + b^2 - c^2) / (2ab)
Trong đó:
- a, b là chừng nhiều năm nhì cạnh của tam giác
- c là chừng nhiều năm cạnh còn sót lại của tam giác
Bước 3: Tính góc thân mật hai tuyến phố thẳng
Sau Lúc tính giá tốt trị của cosin(θ), tao hoàn toàn có thể vận dụng hàm cosine^-1 nhằm tính góc thân mật hai tuyến phố trực tiếp. Kết ngược này tiếp tục mang đến tao góc thân mật hai tuyến phố trực tiếp nhập không khí.
Lưu ý: Để thành phẩm đích, tao cần thiết đáp ứng tính đích chừng nhiều năm những cạnh và vận dụng đích công thức cosin.

Xem thêm: hợp chất hữu cơ la gì

Có nhiều phần mềm của tính góc thân mật hai tuyến phố trực tiếp nhập không khí nhập thực tiễn. Dưới đấy là một số trong những ví dụ:
1. Định vị nhập khối hệ thống xác định toàn thị trường quốc tế (GPS): Trong việc xác xác định trí của một đối tượng người tiêu dùng bên trên mặt phẳng Trái khu đất, tính góc thân mật hai tuyến phố trực tiếp hỗ trợ vấn đề về phía và khoảng cách từ vựng trí lúc này tới điểm đích.
2. Xây dựng và kiến thiết công trình: Trong việc thiết lập chỉnh sửa và xác xác định trí của những bộ phận trong những công việc xây đắp, tính góc thân mật hai tuyến phố trực tiếp được dùng nhằm đo lường và xác lý thuyết.
3. Mô hình hóa ko gian: Trong phân tích và phân tách không khí tía chiều, tính góc thân mật hai tuyến phố trực tiếp vào vai trò cần thiết trong những công việc xác lập côn trùng đối sánh tương quan trong số những đối tượng người tiêu dùng và hình dạng không khí.
4. Định vị nhập điều phối và điều khiển: Trong technology điều phối, tính góc thân mật hai tuyến phố trực tiếp được dùng nhằm xác lý thuyết dịch rời và hùn xác định và tinh chỉnh những phương tiện đi lại như máy cất cánh, tàu thủy hoặc xe pháo tương đối.
5. Xác toan tọa chừng của vật thể: Trong việc xác lập tọa chừng và địa điểm của những vật thể nhập không khí, tính góc thân mật hai tuyến phố trực tiếp được dùng nhằm đo lường và tính toán và xác xác định trí đúng đắn của những vật thể.
Tóm lại, tính góc thân mật hai tuyến phố trực tiếp nhập không khí có tương đối nhiều phần mềm nhập thực tiễn như điều phối, xác định và phân tách không khí, kiến thiết dự án công trình và phân tích khoa học tập.