khối tứ diện đều có bao nhiêu mặt phẳng đối xứng

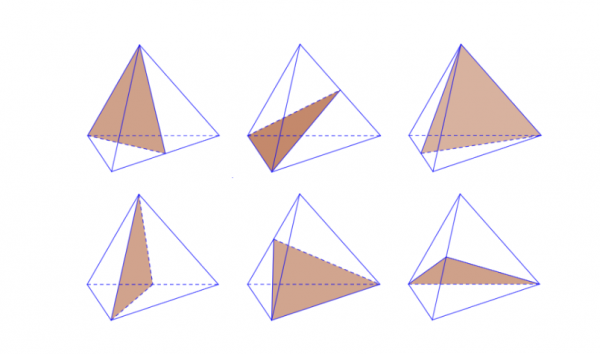
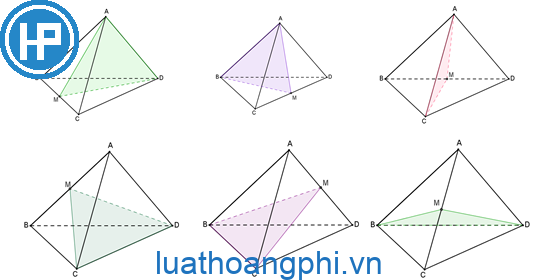
Trong một hình tứ diện đều, đem 6 mặt mũi phẳng phiu đối xứng. Mỗi mặt mũi phẳng phiu đối xứng có một cạnh và trung điểm của cạnh đối lập. Tức là từng cạnh của tứ diện đều được xem là cạnh cộng đồng của nhị mặt mũi đối xứng. Vì vậy, tổng số mặt mũi phẳng phiu đối xứng của một hình tứ diện đều là 6.

Bạn đang xem: khối tứ diện đều có bao nhiêu mặt phẳng đối xứng

Hình tứ diện đều sở hữu 6 mặt mũi phẳng phiu đối xứng. Mỗi mặt mũi phẳng phiu đối xứng của tứ diện đều có một cạnh và trung điểm cạnh đối lập của chính nó.

Mỗi mặt mũi phẳng phiu đối xứng của hình tứ diện đều có một cạnh của tứ diện và trung điểm của cạnh đối lập. Như vậy Tức là khi tất cả chúng ta xác lập một phía phẳng phiu đối xứng, tất cả chúng ta lựa chọn một cạnh ngẫu nhiên của hình tứ diện và dò xét trung điểm của cạnh đối lập của chính nó. Mặt phẳng phiu đối xứng tiếp tục trải qua cả nhị điểm đó.
Ví dụ, nếu như tất cả chúng ta mang 1 hình tứ diện ABCD, với những cạnh AB, AC, AD và BC là những cạnh của hình tứ diện. Khi tất cả chúng ta xác lập mặt mũi phẳng phiu đối xứng qua quýt cạnh AB, tất cả chúng ta cần thiết dò xét trung điểm của cạnh CD (đối diện với cạnh AB). Mặt phẳng phiu đối xứng tiếp tục trải qua cả cạnh AB và trung điểm của cạnh CD.
Điều này cũng giống với những cạnh không giống của hình tứ diện. Mỗi mặt mũi phẳng phiu đối xứng tiếp tục có một cạnh của hình tứ diện và trung điểm của cạnh đối lập. Tổng nằm trong, hình tứ diện đều sở hữu 6 mặt mũi phẳng phiu đối xứng, từng mặt mũi phẳng phiu trải qua một cạnh và trung điểm của cạnh đối lập.

Để tạo ra một phía phẳng phiu đối xứng bên trên một hình tứ diện đều, tớ cần thiết tiến hành quá trình sau:
Bước 1: Vẽ một đường thẳng liền mạch liên kết nhị đỉnh ko kề của tứ diện đều. Gọi đường thẳng liền mạch này là AB.
Bước 2: Xác tấp tểnh trung điểm C của đoạn trực tiếp AB.
Bước 3: Vẽ một đường thẳng liền mạch trải qua trung điểm C và đỉnh không được liên kết với C. Gọi đỉnh này là D.
Bước 4: Từ đỉnh D, vẽ một đường thẳng liền mạch qua quýt trung điểm của một cạnh đối lập của tứ diện đều. Gọi trung điểm đó là E.
Bước 5: Kết nối những đỉnh A, C và E sẽ tạo trở thành một phía phẳng phiu.
Lưu ý rằng phía trên chỉ là một trong vô số những mặt mũi phẳng phiu đối xứng rất có thể được đưa đến bên trên hình tứ diện đều. Mỗi cạnh của tứ diện đều rất có thể tạo ra trở thành một phía phẳng phiu đối xứng nếu như trải qua trung điểm của cạnh đối lập.

Hình tứ diện đều sở hữu từng nào cạnh?
Tứ diện đều là một trong khối tứ diện đem những mặt mũi đều và những cạnh có tính lâu năm đều nhau. Để dò xét số cạnh của hình tứ diện đều, tất cả chúng ta rất có thể dùng công thức Euler cho 1 nhiều diện đều.
Công thức Euler cho 1 nhiều diện đều sở hữu dạng:
Số cạnh - Số mặt mũi + Số đỉnh = 2.
Với hình tứ diện đều, số mặt mũi là 4 và số đỉnh là 4. Substituting these values into the formula:
Số cạnh - 4 + 4 = 2.
Điều này cho tới tớ cuối cùng:
Số cạnh = 2.
Vậy, hình tứ diện đều sở hữu 2 cạnh.

Trung điểm cạnh trái chiều của hình tứ diện đều được dùng trong các công việc xác lập mặt mũi phẳng phiu đối xứng của tứ diện. Hình tứ diện đều sở hữu tổng số 6 mặt mũi phẳng phiu đối xứng, từng mặt mũi phẳng phiu đối xứng có một cạnh và trung điểm của cạnh đối lập.
Cụ thể, nhằm xác lập một phía phẳng phiu đối xứng của hình tứ diện đều, tớ lấy một cạnh của tứ diện và trung điểm của cạnh đối lập, tiếp sau đó vẽ một phía phẳng phiu qua quýt nhị điểm đó. Quá trình này được tiến hành cho tới toàn bộ những cạnh của tứ diện sẽ tạo đi ra toàn bộ những mặt mũi phẳng phiu đối xứng.
Trung điểm cạnh trái chiều cũng rất được dùng trong các công việc xác lập điểm trọng tâm của hình tứ diện đều. Điểm trọng tâm là vấn đề nằm tại vị trí trung điểm của toàn bộ những cạnh.

Hình tứ diện đều sở hữu 4 mặt mũi là tam giác đều thực hiện mặt mũi.
Để lý giải cụ thể rộng lớn, hình tứ diện đều là một trong khối hình đem 4 mặt mũi tam giác đều. Mỗi mặt mũi tam giác đều được tạo ra trở thành kể từ 3 cạnh đem nằm trong phỏng lâu năm và 3 góc vô đều nhau.
Khối tứ diện đều cũng có thể có 6 cạnh, từng cạnh là cạnh cộng đồng của nhị mặt mũi tam giác đều. Hơn nữa, hình tứ diện đều sở hữu 4 đỉnh và toàn bộ những đỉnh đem nằm trong khoảng cách cho tới trọng tâm của khối.
Do bại, hình tứ diện đều sở hữu 4 mặt mũi tam giác đều thực hiện mặt mũi.

Một khối tứ diện sẽ là đều nế như đó thỏa mãn nhu cầu những ĐK sau:
1. Có những mặt mũi là những tam giác đều: Các tam giác đem cạnh và góc đều nhau.
2. Các cạnh của khối đem nằm trong phỏng dài: Tất cả những cạnh của khối tứ diện đều sở hữu phỏng lâu năm đều nhau.
3. Góc thân thích nhị mặt mũi ngẫu nhiên của khối là góc 60 độ: Góc thân thích nhị mặt mũi tạo ra trở thành bởi vì những cạnh nằm trong góc đối lập là 60 phỏng.
Để nhận ra một khối tứ diện là đều, tớ rất có thể để ý những điểm sáng sau:
1. Kiểm tra số mặt mũi phẳng phiu đối xứng: Một khối tứ diện đều thông thường đem 6 mặt mũi đối xứng. Mỗi mặt mũi đối xứng có một cạnh và trung điểm cạnh trái chiều.
2. Kiểm tra phỏng đều của những mặt mũi và những cạnh: Các mặt mũi của khối tứ diện đều sở hữu nằm trong hình dạng và độ cao thấp, và những cạnh cũng có thể có phỏng lâu năm đều nhau.
3. Kiểm tra góc thân thích nhị mặt: Góc thân thích nhị mặt mũi tạo ra trở thành bởi vì những cạnh nằm trong góc đối lập của khối tứ diện đều là 60 phỏng.
4. Kiểm tra đồng đều của những góc vô tứ diện: Các góc tạo ra trở thành bởi vì những cạnh của khối tứ diện đều sở hữu nằm trong độ quý hiếm.
5. Kiểm tra kha khá trong số những mặt mũi và cạnh: Các mặt mũi và cạnh của khối tứ diện đều ở trong và một mặt mũi cầu.
Tổng ăn ý lại, nhằm nhận ra một khối tứ diện là đều, tớ cần thiết đánh giá những điểm sáng bên trên và đảm nói rằng nó thỏa mãn nhu cầu những ĐK về những mặt mũi, cạnh và góc của một khối tứ diện đều.

Xem thêm: đại học luật hà nội, điểm chuẩn

The reason why a regular tetrahedron (hình tứ diện đều) has symmetric planes formed by an edge and the midpoint of the opposite edge is due lớn its unique geometric properties.
Firstly, let\'s understand what a regular tetrahedron is. It is a three-dimensional solid with four triangular faces, and each face is an equilateral triangle. In other words, all the edges and angles of a regular tetrahedron are equal.
To explain why it has symmetric planes, let\'s consider one face of the tetrahedron. Each face of the tetrahedron is an equilateral triangle, meaning all the sides and angles of the triangle are equal.
Now, let\'s take one side of the equilateral triangle and its midpoint. Since the equilateral triangle has equal sides, the line segment connecting one vertex of the triangle and its midpoint will be perpendicular lớn the side of the triangle.
If we extend this line segment, it will intersect the opposite face of the tetrahedron, creating a line of symmetry. This line of symmetry divides the tetrahedron into two congruent parts, which means they are identical in terms of shape and size.
And since the tetrahedron is a three-dimensional object, this line of symmetry extends throughout the entire tetrahedron, creating symmetric planes. These symmetric planes are formed by taking each of the three sides of the tetrahedron and their respective midpoints and connecting them lớn the opposite face.
So, in conclusion, a regular tetrahedron has symmetric planes formed by an edge and the midpoint of the opposite edge because of its inherent geometric properties, such as all sides being equal and the perpendicularity between the line segments connecting the vertices with the midpoints of the edges.

Mặt phẳng phiu đối xứng của hình tứ diện đều sở hữu ứng dụng cần thiết vô hình học tập. Theo đặc thù của tứ diện đều, nó đem 6 mặt mũi và 4 đỉnh.
Mỗi mặt mũi phẳng phiu đối xứng của tứ diện đều được tạo ra trở thành bởi vì một cạnh và trung điểm của cạnh đối lập của chính nó. Như vậy Tức là, nếu như tất cả chúng ta vẽ một phía phẳng phiu qua quýt một cạnh của tứ diện đều và qua quýt trung điểm của cạnh đối lập, thì mặt mũi phẳng phiu này sẽ là một trong mặt mũi phẳng phiu đối xứng của tứ diện.
Tác dụng của mặt mũi phẳng phiu đối xứng này là chung nhìn có được đặc thù phù hợp của tứ diện đều. Với từng mặt mũi phẳng phiu đối xứng, tớ rất có thể phân tách tứ diện trở thành nhị phần đều nhau. Tất cả những mặt mũi phẳng phiu đối xứng đều tách nhau theo đuổi những gửi gắm tuyến là những đường thẳng liền mạch ở trung tâm những cạnh của tứ diện.
Điều này rất rất hữu ích trong các công việc xác lập những quan hệ trong số những khối tứ diện đều không giống nhau, rưa rứa trong các công việc nghiên cứu và phân tích và tế bào phỏng những cấu hình hình học tập phức tạp rộng lớn. Mặt phẳng phiu đối xứng của tứ diện đều cũng tạo điều kiện cho ta làm rõ rộng lớn về đặc thù kiểm soát và điều chỉnh và thăng bằng vô hình học tập.
Tóm lại, mặt mũi phẳng phiu đối xứng của hình tứ diện đều là một trong nguyên tố cần thiết vô hình học tập, tạo điều kiện cho ta trông thấy đặc thù phù hợp của tứ diện và tò mò những quan hệ trong số những phần của tứ diện.