Ở công tác Toán đại số lớp 12, kỹ năng về nguyên hàm e mũ u và những hàm số giản dị và đơn giản nhập vai trò trung tâm trong những kỳ ganh đua. Để thăm dò hiểu thâm thúy rộng lớn về nội dung này, những em hãy tham khảo ngay lập tức nội dung bài viết tiếp sau đây kể từ Marathon Education.
>>> Xem thêm: Toán 12 Nguyên Hàm – Lý Thuyết Và Một Số Bài Tập Ví Dụ
Bạn đang xem: nguyên hàm e mũ u
Lý thuyết nguyên vẹn hàm
Định nghĩa nguyên vẹn hàm
Ta có: ký hiệu K là đoạn, nửa khoảng tầm hoặc khoảng tầm của tập dượt R.
Cho hàm số f(x) đã và đang được xác lập bên trên K, nếu như F’(x) = f(x) với từng độ quý hiếm x ∈ K, tớ hoàn toàn có thể xác định rằng F(x) được gọi là nguyên vẹn hàm của hàm số f(x).
Một số tấp tểnh lý về nguyên vẹn hàm:
- Trong tình huống F(x) được xác lập là một trong những nguyên vẹn hàm của hàm số f(x) bên trên tập K thì với hằng số C ngẫu nhiên, tớ đều có: G(x) = F(x)+C cũng khá được coi là một trong những nguyên vẹn hàm của hàm số f(x) bên trên K.
- Ngược lại, nếu như F(x) được xác lập là một trong những nguyên vẹn hàm của hàm số f(x) bên trên K thì toàn bộ những nguyên vẹn hàm của hàm số f(x) bên trên tập dượt K nhằm hoàn toàn có thể được viết lách bên dưới dạng F(x) + C (với độ quý hiếm C là một trong những hằng số bất kỳ). Ta sở hữu, ký hiệu chúng ta nguyên vẹn hàm của hàm số f(x) là ∫f(x)dx. Theo cơ, ∫f(x)dx =F(x) + C, C ∈ R.
Tính hóa học của nguyên vẹn hàm
Liên quan lại cho tới khái niệm gần giống tấp tểnh lý về nguyên vẹn hàm, những em cũng rất cần được ghi lưu giữ một vài đặc điểm cần thiết như sau:
- ∫f(x)dx = F(x) + C, C ∈ R.
- ∫kf(x)dx = k ∫f(x)dx (với k là hằng số không giống 0)
- ∫(f(x) ± g(x)) = ∫f(x)dx ± ∫g(x)dx.

Lý thuyết hàm số mũ
Trước Khi cút nhập phần lý thuyết về nguyên hàm e mũ u, những em rất cần được cầm vững chắc một vài phần kỹ năng trọng tâm về hàm số nón như sau:
Định nghĩa hàm số mũ
Hàm số nón được khái niệm là hàm số ở dạng nó = ax với ĐK thông số a luôn luôn dương và không giống độ quý hiếm 1.
Xem thêm: chức năng của tuyến tụy
Tính hóa học hàm số mũ
Hàm số nón nó = ax (a>0, a1) tiếp tục tồn bên trên một vài đặc điểm như sau:
- Hàm số nón sở hữu tập dượt xác lập là R.
- x ∈ R, tớ sở hữu đạo hàm của hàm số nón nó = ax được xem là y′ = axlna.
- Xét về chiều trở nên thiên của hàm số nón, tớ có:
- Nếu a > 1 thì hàm số tiếp tục luôn luôn đồng trở nên.
- Trường thích hợp 0 < a < 1 thì hàm số tiếp tục luôn luôn nghịch tặc trở nên.
- Trục Ox được xem là lối tiệm cận ngang của đồ dùng thị.
- Đồ thị tiếp tục ở trọn vẹn phía bên trên của trục hoành (y = ax > 0 ∀x). Đồng thời, đồ dùng thị hàm số nón tiếp tục luôn luôn hạn chế trục tung bên trên điểm (0;1) và trải qua điểm (1;a).
>>> Xem thêm: Lý Thuyết Và Đồ Thị Của Hàm Số Mũ, Hàm Số Lôgarit
Hằng số e nhập toán học tập là gì?
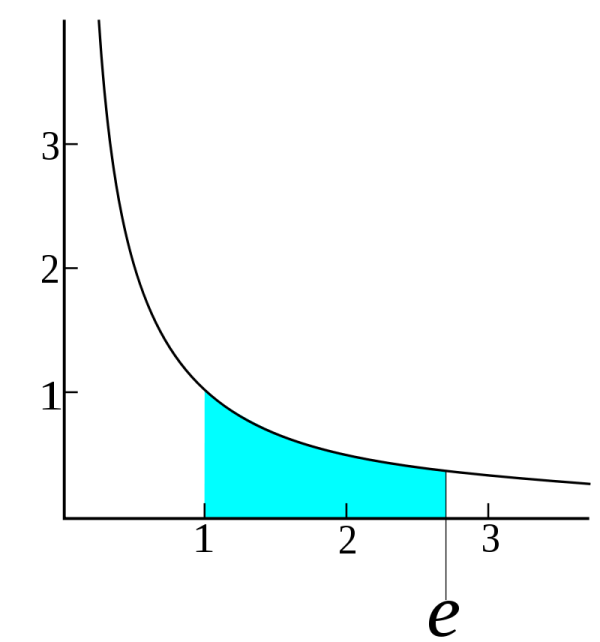
Số e là một trong những hằng số toán học tập có mức giá trị ngay gần vì như thế với 2,71828… Hằng số này hoàn toàn có thể được trình diễn ở vô số cách không giống nhau. Cụ thể:
\begin{aligned}
&\footnotesize\bull\text{Số e là số thực dương có một không hai tuy nhiên độ quý hiếm của đạo hàm của hàm số nón cơ số }\\
&\footnotesize\text{e cũng chủ yếu vì như thế hàm số đó: }\frac{d}{dt}e^t=e^t.\\
&\footnotesize\bull\text{Số e là số thực dương có một không hai tuy nhiên } \frac{d}{dt}log_et=\frac{1}{t}.\\
&\footnotesize\bull\text{Số e là số lượng giới hạn của }(1 + \frac{1}{n})^n \text{ Khi n tiến bộ về vô cực kì }e = \lim\limits_{n \to \infin}(1 + \frac{1}{n})^n.\\
&\footnotesize\bull\text{Số e cũng chính là tổng của chuỗi vô hạn nhập cơ n! là giai quá của n: }\\
&\footnotesize\sum^e_{n=0}\frac{1}{n!}=\frac{1}{0!}+\frac{1}{1!}+ \frac{1}{2!}+\frac{1}{3!}+...\\
&\footnotesize\bull\text{Số e là số thực dương có một không hai tuy nhiên }\int_1^e\frac{1}{t}dt=1. \text{ Nghĩa là diện tích S hình }\\
&\footnotesize\text{phẳng được số lượng giới hạn vì như thế đồ dùng thị hàm số }y=\frac{1}{t} \text{từ t = 1 cho tới t = e sẽ sở hữu diện }\\
&\footnotesize\text{tích vì như thế 1.}
\end{aligned}
Bảng những công thức tính nguyên hàm e mũ u
Để tính được nguyên hàm e mũ u, những em hoàn toàn có thể vận dụng một vài công thức nguyên vẹn hàm trải qua những bảng nguyên hàm e mũ u cơ phiên bản và phối kết hợp như sau:
Bảng nguyên vẹn hàm e nón cơ bản
\begin{aligned}
\hline
\begin{array}{|cc|}
&1. \int e^xdx=e^x+C\\ \hline
&2. \int e^udu=e^u+C \\ \hline
&3. \int e^{ax+b}dx=e^{ax+b}+C \\ \hline
&4. \int e^{-x}dx=-e^{-x}+C \\ \hline
&5. \int e^{-u}dx=-e^{-u}+C \\ \hline
\end{array}
\end{aligned}
Bảng nguyên vẹn hàm e nón kết hợp
\def\arraystretch{1.5}
\begin{aligned}
\hline
\begin{array}{|cc|}
&6. \int cos(ax).e^{bx}=\frac{(asin(ax)+bcos(ax)).e^{bx}}{a^2+b^2}+C\\ \hline
&7. \int cos(au).e^{bu}=\frac{(bsin(au)-acos(au)).e^{bu}}{a^2+b^2}+C\\ \hline
&8. \int e^{au}du=\frac{e^{au}}{a}+C \\ \hline
&9. \int u.e^{au}du=(\frac{u}{a}-\frac{1}{a^2})e^{au}+C \\ \hline
&10. \int u^ne^{au}du=\frac{u^ne^{au}}{a}-\frac{n}{a} \int u^{n-1}e^{au}du+C
\\\hline
\end{array}
\end{aligned}
>>> Xem thêm: Tính Nguyên Hàm Ln x. Bài Tập Vận Dụng Có Lời Giải Chi Tiết
Xem thêm: phép vua thua lệ làng
Tham khảo ngay lập tức những khoá học tập online của Marathon Education
Trên đó là những vấn đề tương quan cho tới nguyên hàm e mũ u và những hàm số giản dị và đơn giản. Hy vọng qua quýt nội dung bài viết này, những em tiếp tục “bỏ túi” được không ít kỹ năng có ích và mới nhất mẻ.
Hãy contact ngay lập tức với Marathon và để được tư vấn nếu như những em mong muốn học trực tuyến nâng lên kỹ năng nhé! Marathon Education chúc những em được điểm trên cao trong những bài bác đánh giá và kỳ ganh đua chuẩn bị tới!











Bình luận