Tính hóa học tam giác vuông - Tắc quyết dò thám hiểu những điều thú vị
Chủ đề Tính hóa học tam giác vuông: Tam giác vuông là một trong hình học tập hữu ích và thú vị nhập toán học tập. Nó có rất nhiều đặc điểm đặc biệt quan trọng canh ty tất cả chúng ta hiểu sâu sắc rộng lớn về hình dạng và những tấp tểnh lý tương quan. Một nhập số này là đặc điểm nhị góc nhọn phụ nhau và đặc điểm bình phương cạnh huyền. Nhờ những đặc điểm này, tất cả chúng ta rất có thể đơn giản dò thám rời khỏi những vấn đề cần thiết và vận dụng nó vào giải toán. Vì vậy, mày mò và nghiên cứu và phân tích về tính chất tam giác vuông là một trong thưởng thức ấn tượng và mê hoặc.
Bạn đang xem: tính chất tam giác vuông
Tam giác vuông đem những đặc điểm sau:
1. Tam giác mang trong mình một góc vuông là tam giác vuông.
2. Tam giác đem nhị góc nhọn phụ nhau là tam giác vuông.
3. Tam giác đem cạnh huyền, cạnh đối lập với góc vuông, là cạnh nhiều năm nhất nhập tam giác vuông.
4. Tam giác vuông đem cạnh góc vuông là nửa chu vi của tam giác.
5. Bình phương của cạnh huyền vì chưng tổng bình phương của nhị cạnh góc vuông.
6. Tổng phỏng nhiều năm nhị cạnh góc vuông là lớn số 1 vào cụ thể từng tổng phỏng nhiều năm nhị cạnh nhập tam giác vuông.
7. Một tam giác rất có thể được xem như là tam giác vuông nếu như và chỉ nếu như tổng bình phương của nhị cạnh góc vuông vì chưng bình phương của cạnh huyền.
8. Đối xứng qua chuyện đàng trung tuyến trải qua góc vuông, tam giác vuông không thay đổi những đặc điểm và hình dạng.
9. Hai tam giác vuông đem cạnh huyền và một cạnh góc vuông đều bằng nhau là tam giác vuông đồng dạng.
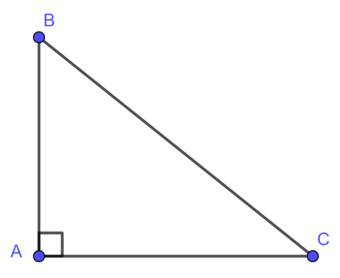
Tam giác vuông đem tổng những góc vì chưng bao nhiêu?
Tam giác vuông đem tổng những góc vì chưng 180 phỏng.
Giải thích:
- Định nghĩa tam giác vuông: Tam giác mang trong mình một góc vì chưng 90 phỏng được gọi là tam giác vuông.
- Tính hóa học tam giác vuông: Trong tam giác vuông, tổng những góc vì chưng 180 phỏng.
Vì tam giác vuông mang trong mình một góc vì chưng 90 phỏng, và tổng số đem 3 góc nhập một tam giác, nên nhị góc sót lại nhập tam giác vuông cũng
phải nằm trong lại nhằm đạt tổng 180 phỏng.
Tam giác vuông đem từng nào cạnh?
Tất cả tam giác vuông đều phải sở hữu tía cạnh.
Cạnh Huyền Tam Giác Vuông - 3 Cách Tính - Toán Học
Tính hóa học tam giác vuông: Cùng mày mò đặc điểm đặc biệt quan trọng của tam giác vuông và dò thám hiểu về mối quan hệ trong số những góc và cạnh nhập tam giác này. Đừng bỏ qua đoạn phim này nhằm làm rõ rộng lớn về tam giác vuông!
Đồng Dạng của Tam Giác Vuông - Bài 8 - Toán Học 8 - Cô Phạm Huệ Chi (Dễ Hiểu Nhất)
Đồng dạng của tam giác vuông: Thậm chí cả tam giác vuông cũng rất có thể đồng dạng với nhau! Hãy theo đòi dõi đoạn phim này nhằm mày mò những quy tắc đồng dạng đặc biệt quan trọng của tam giác vuông và vận dụng nó vào giải những bài xích luyện thú vị!
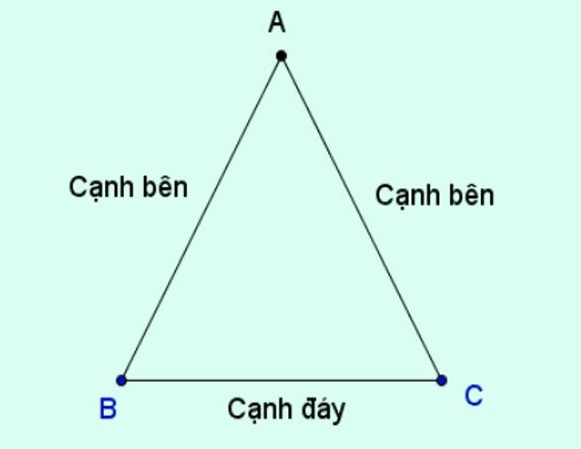
Tên gọi của cạnh đối lập với góc vuông nhập tam giác vuông là gì?
Tên gọi của cạnh đối lập với góc vuông nhập tam giác vuông được gọi là cạnh huyền.
Tên gọi của nhị cạnh kề với góc vuông nhập tam giác vuông là gì?
Tên gọi của nhị cạnh kề với góc vuông nhập tam giác vuông là cạnh góc và cạnh huyền.
_HOOK_
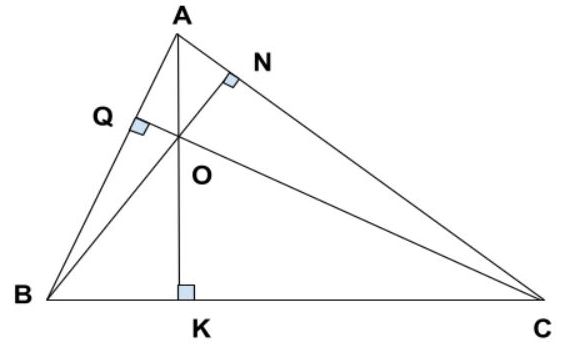
Tam giác vuông đem những đàng cao nào?
Tam giác vuông đem tía đàng cao, bao gồm đàng cao kẻ kể từ đỉnh vuông cho tới cạnh huyền (cạnh đối lập với góc vuông) và hai tuyến phố cao kẻ kể từ đỉnh vuông cho tới nhị đỉnh sót lại bên trên cạnh góc vuông.
Tam giác vuông đem tâm đàng tròn xoe nước ngoài tiếp hoặc không?
Để vấn đáp thắc mắc này, tớ nên biết rằng tam giác vuông mang trong mình một góc vuông. Tính hóa học của đàng tròn xoe nước ngoài tiếp tam giác là đàng tròn xoe trải qua những tía đỉnh của tam giác bại.
Vậy nhằm xác lập coi tam giác vuông đem tâm đàng tròn xoe nước ngoài tiếp hay là không, tớ cần thiết đánh giá coi tía đỉnh của tam giác vuông đem trực tiếp sản phẩm hay là không. Nếu tía đỉnh của tam giác vuông ko trực tiếp sản phẩm, tức là không tồn tại đàng tròn xoe nước ngoài tiếp trải qua tam giác vuông bại.
Tuy nhiên, việc tam giác vuông đem tâm đàng tròn xoe nước ngoài tiếp hay là không còn tùy theo những đặc điểm không giống của tam giác và ví dụ rộng lớn là địa điểm đỉnh vuông của tam giác. Để đáp ứng đặc điểm này, tớ cần thiết đánh giá coi tam giác vuông đem tâm đàng tròn xoe nước ngoài tiếp hay là không.
Tính hóa học của nhị góc nhọn nhập tam giác vuông là gì?
Tính hóa học của nhị góc nhọn nhập tam giác vuông là:
1. Hai góc nhọn nhập tam giác vuông luôn luôn phụ nhau. Như vậy tức là tổng kích cỡ của nhị góc nhọn luôn luôn vì chưng 90 phỏng, còn được gọi là góc vuông. Chẳng hạn, nếu như một góc nhọn nhập tam giác vuông có tính rộng lớn là 30 phỏng, thì góc nhọn sót lại sẽ sở hữu kích cỡ là 60 phỏng.
2. Một đặc điểm không giống của nhị góc nhọn nhập tam giác vuông là bình phương của một cạnh huyền (cạnh đối lập với góc vuông) vì chưng tổng bình phương của nhị cạnh kề với góc vuông. Như vậy rất có thể được trình diễn bằng phương pháp dùng tấp tểnh lý Pythagoras. Ví dụ, nếu như phỏng nhiều năm nhị cạnh kề với góc vuông là 3 và 4, thì bình phương của cạnh huyền được xem là 3^2 + 4^2 = 9 + 16 = 25.
Những đặc điểm này canh ty tất cả chúng ta hiểu và giải quyết và xử lý những câu hỏi tương quan cho tới tam giác vuông một cơ hội hiệu suất cao.
Xem thêm: ngày xuân con én đưa thoi
Toán Lớp 9 | Hình 1: Hệ Thức Lượng nhập Tam Giác Vuông
Hệ thức lượng nhập tam giác vuông: Hãy coi đoạn phim này nhằm mày mò những hệ thức lượng thú vị nhập tam giác vuông. Từ công thức đặc biệt quan trọng của sin, cos và tan cho tới công thức Pythagoras, các bạn sẽ biết phương pháp vận dụng nó vào giải những bài xích luyện tam giác vuông!
Hệ Thức về Cạnh và Đường Cao nhập Tam Giác Vuông - Bài 1 - Toán 9 - Cô Huệ Chi (Hay Nhất)
Hệ thức về cạnh và đàng cao nhập tam giác vuông: Những hệ thức về cạnh và đàng cao nhập tam giác vuông tiếp tục khiến cho bạn giải quyết và xử lý những bài xích luyện về tam giác hiệu suất cao hơn! Hãy dò thám hiểu cụ thể về bọn chúng bằng phương pháp coi đoạn phim này!
Tính hóa học của bình phương cạnh huyền nhập tam giác vuông là gì?
Tính hóa học của bình phương cạnh huyền nhập tam giác vuông là bình phương của cạnh huyền vì chưng tổng bình phương nhị cạnh góc vuông. Để minh chứng điều này, tất cả chúng ta rất có thể vận dụng tấp tểnh lý Pythagoras nhập tam giác vuông.
Định lý Pythagoras bảo rằng nhập một tam giác vuông, bình phương của cạnh huyền (cạnh đối lập với góc vuông) vì chưng tổng bình phương của nhị cạnh góc vuông. Để gọi tam giác vuông là ABC, tất cả chúng ta có:
AB^2 = AC^2 + BC^2
Ở trên đây, AB là cạnh huyền, còn AC và BC theo thứ tự là nhị cạnh góc vuông. Tuy nhiên, theo đòi đặc điểm của tam giác vuông, tất cả chúng ta hiểu được AC và BC đều là cạnh góc vuông. Do bại, tớ rất có thể bịa AC = a và BC = b nhằm đơn giản viết lách công thức.
Vì vậy, công thức trở nên AB^2 = a^2 + b^2. Như vậy, tớ đem đặc điểm của bình phương cạnh huyền nhập tam giác vuông là bình phương của cạnh huyền vì chưng tổng bình phương nhị cạnh góc vuông: AB^2 = a^2 + b^2.

Tam giác vuông đem bình phương của một cạnh vì chưng bao nhiêu?
Tam giác vuông đem bình phương của một cạnh vì chưng tổng bình phương nhị cạnh góc vuông sót lại. Để tính được bình phương của một cạnh nhập tam giác vuông, tớ rất có thể vận dụng tấp tểnh lý Pythagoras.
Định lý Pythagoras: Trong một tam giác vuông, bình phương của cạnh huyền (cạnh đối lập góc vuông) vì chưng tổng bình phương nhị cạnh góc vuông sót lại.
Với tam giác vuông ABC, tớ đem cạnh huyền là AB (đối diện góc vuông), và nhị cạnh góc vuông sót lại là AC và BC. sát dụng tấp tểnh lý Pythagoras:
AB^2 = AC^2 + BC^2
Do bại, bình phương của cạnh AB (cạnh huyền) nhập tam giác vuông vì chưng tổng bình phương nhị cạnh góc vuông sót lại, tức là AC^2 + BC^2.
_HOOK_
Tính hóa học của tam giác vuông tương quan cho tới đàng tròn xoe nước ngoài tiếp là gì?
Tính hóa học của tam giác vuông tương quan cho tới đàng tròn xoe nước ngoài tiếp là: đàng tròn xoe nước ngoài tiếp tam giác vuông đem 2 lần bán kính vì chưng cạnh huyền của tam giác. Để minh chứng điều này, tớ rất có thể tuân theo công việc sau:
Bước 1: Xác tấp tểnh tam giác vuông ABC đem góc vuông bên trên A, với cạnh huyền BC.
Bước 2: Vẽ đàng vuông góc trải qua trung điểm của cạnh huyền BC, gọi là đường thẳng liền mạch DE.
Bước 3: Đường trực tiếp DE phân chia cạnh huyền BC trở nên nhị phần đều bằng nhau.
Bước 4: Khi bại, A là trung điểm của cạnh sót lại, gọi là AD.
Bước 5: Khi bại, tớ đem AB = AD = AC (do A là trung điểm của cạnh còn lại).
Bước 6: Suy rời khỏi, tam giác ABC là tam giác đều.
Bước 7: Vì tam giác ABC là tam giác đều, nên tớ rất có thể xác lập được đàng tròn xoe nước ngoài tiếp tam giác bằng phương pháp lấy đàng trung trực của cạnh BC, tức là đàng vuông góc AB và AC bên trên B và C.
Bước 8: Đường trung trực của cạnh BC là đàng vuông góc AB và AC bên trên B và C đó là đoạn trực tiếp DE vừa mới được vẽ.
Bước 9: Trung điểm của cạnh BC là vấn đề phía trên đàng trung trực của BC, đặc điểm đó đó là tâm O của đàng tròn xoe xung quanh tam giác ABC.
Bước 10: Vì vậy, tớ tóm lại rằng đàng tròn xoe nước ngoài tiếp tam giác vuông đem 2 lần bán kính vì chưng cạnh huyền của tam giác.
Tính hóa học của tam giác vuông tương quan cho tới đàng tròn xoe nội tiếp là gì?
Tính hóa học của tam giác vuông tương quan cho tới đàng tròn xoe nội tiếp là: Tam giác vuông mang trong mình một đàng tròn xoe được vẽ xúc tiếp bên cạnh đó với tía cạnh của tam giác. Điểm xúc tiếp của đàng tròn xoe với cạnh huyền của tam giác là trung điểm của cạnh bại. Đường tròn xoe nội tiếp tam giác vuông cũng trải qua nhị đỉnh vuông góc cùng nhau của tam giác và tâm của đàng tròn xoe nội tiếp trùng với đỉnh góc vuông của tam giác. Đồng thời, nửa đường kính của đàng tròn xoe nội tiếp tam giác vuông vì chưng 50% cạnh huyền của tam giác.
Tam giác vuông đem trung điểm của những cạnh đều bằng nhau hoặc không?
Tam giác vuông không tồn tại trung điểm của những cạnh đều bằng nhau. Để phân tích và lý giải điều này, tất cả chúng ta cần thiết kiểm tra những đặc điểm của tam giác vuông.
1. Tam giác vuông mang trong mình một góc vuông, gọi là góc vuông.
2. Tam giác vuông đem tía cạnh, nhập bại cạnh đối lập với góc vuông được gọi là cạnh huyền, còn nhị cạnh sót lại được gọi là cạnh góc vuông.
3. Theo tấp tểnh lý Pythagoras, bình phương cạnh huyền vì chưng tổng bình phương nhị cạnh góc vuông.
Giả sử cạnh huyền của tam giác vuông là c, và nhị cạnh góc vuông theo thứ tự là a và b. Theo đặc điểm 3, tớ đem phương trình: c^2 = a^2 + b^2.
Nếu tam giác vuông đem trung điểm của những cạnh đều bằng nhau, tức là a = b = c/2.
Thay nhập phương trình bên trên, tớ được: (c/2)^2 = (c/2)^2 + (c/2)^2 => c^2/4 = c^2/4 + c^2/4 => c^2/4 = c^2/2.
Phương trình bên trên ko đích thị với ngẫu nhiên độ quý hiếm này của c, chính vì vậy giả thiết thuở đầu là sai.
Do bại, tam giác vuông không tồn tại trung điểm của những cạnh đều bằng nhau.

Hệ Thức về Cạnh và Đường Cao nhập Tam Giác Vuông - Thầy Nguyễn Cao Cường
Thầy Nguyễn Cao Cường: Hãy nằm trong học tập và mày mò trái đất toán học tập nằm trong thầy Nguyễn Cao Cường! Với phong thái dạy dỗ vui nhộn và những phân tích và lý giải giản dị và đơn giản, thầy tiếp tục khiến cho bạn hiểu và yêu thương mến môn toán rộng lớn lúc nào không còn. Hãy coi đoạn phim này nhằm thưởng thức sự phát minh và hăng hái của thầy!
Tính hóa học của đàng cao so với cạnh huyền nhập tam giác vuông là gì?
Tính hóa học của đàng cao so với cạnh huyền nhập tam giác vuông là:
Trong tam giác vuông ABC, nếu như AD là đàng cao kẻ kể từ đỉnh A xuống cạnh BC (cạnh huyền), thì tớ đem đặc điểm sau:
1. Độ nhiều năm đàng cao (AD) phân chia cạnh huyền (BC) trở nên nhị phần đem tỷ trọng vì chưng phỏng nhiều năm phần sót lại của cạnh huyền (BC) đối với tổng phỏng nhiều năm nhị cạnh góc vuông.
Điều này rất có thể được trình diễn vì chưng công thức:
AD/BC = BC/AB + BC/AC
Hay hay còn gọi là tấp tểnh lí Pythagoras với công thức:
AD^2 = AB * AC
Tính hóa học này canh ty tất cả chúng ta tính phỏng nhiều năm của đàng cao (AD) lúc biết phỏng nhiều năm của nhị cạnh góc vuông (AB và AC).
Xem thêm: bộ đề thi bằng lái xe a1
Tam giác vuông đem tỷ trọng trong số những cạnh như vậy nào?
Trong một tam giác vuông, tỷ trọng trong số những cạnh được xác lập vì chưng tấp tểnh lý Pythagoras. Định lý Pythagoras cho là nhập một tam giác vuông, bình phương cạnh huyền (cạnh đối lập với góc vuông) vì chưng tổng bình phương nhị cạnh góc.
Cụ thể, nếu như tất cả chúng ta ký hiệu cạnh huyền là c và nhị cạnh góc theo thứ tự là a và b, thì theo đòi tấp tểnh lý Pythagoras, tớ đem công thức: c^2 = a^2 + b^2. Đây là công thức cơ bạn dạng nhằm tính tỷ trọng trong số những cạnh nhập một tam giác vuông.
Ví dụ, nếu như tớ biết độ quý hiếm của nhị cạnh góc là a = 3 và b = 4, tớ rất có thể sử dụng công thức bên trên nhằm tính độ quý hiếm của cạnh huyền c: c^2 = 3^2 + 4^2 = 9 + 16 = 25. Rút căn mặt mũi nhị của tất cả nhị vế của phương trình, tớ cảm nhận được c = 5. Do bại, nhập tình huống này, tỷ trọng trong số những cạnh là a : b : c = 3 : 4 : 5.
Tuy nhiên, cần thiết chú ý rằng tỷ trọng trong số những cạnh rất có thể thay cho thay đổi tùy nằm trong nhập độ quý hiếm của a và b. Mỗi tam giác vuông mang trong mình một tỷ trọng riêng biệt, và tấp tểnh lý Pythagoras chỉ mang đến tất cả chúng ta biết mối quan hệ trong số những cạnh nhập một tam giác vuông ví dụ.
_HOOK_
Hình học tập 9 - Bài 1: Hệ thức lượng nhập tam giác vuông (mới nhất 2022)
Tìm hiểu về những hình học tập căn bạn dạng và vận dụng nó vào giải câu hỏi thực tiễn. Xem ngay lập tức nhằm trở nên Chuyên Viên hình học! Bài 1: Hãy nằm trong mày mò những hệ thức lượng thú vị nhập bài











Bình luận