Bài viết lách trình diễn cách thức xác lập và tính góc thân thích hai tuyến phố trực tiếp chéo cánh nhau nhập không khí bằng phương pháp dùng hình học tập không khí truyền thống, đấy là một nội dung thông thường gặp gỡ nhập lịch trình Hình học tập 11 chương 3: Quan hệ vuông góc, kỹ năng và những ví dụ nhập nội dung bài viết được xem thêm kể từ những tư liệu hình học tập không khí được share bên trên TOANMATH.com.
Bài toán: Cho hai tuyến phố trực tiếp $a$ và $b$ chéo cánh nhau, xác lập góc thân thích $2$ đường thẳng liền mạch $a$ và $b.$
Bạn đang xem: tính góc giữa hai đường thẳng lớp 11
Để xác lập góc thân thích hai tuyến phố trực tiếp $a$ và $b$ chéo cánh nhau, tao dùng những cơ hội sau:
Cách 1: Chọn hai tuyến phố thẳng tách nhau $a’$ và $b’$ thứu tự song song với $a$ và $b$. Khi bại liệt $(\widehat {a,b}) = (\widehat {a’,b’})$.
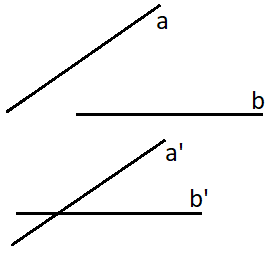
Cách 2: Chọn một điểm $A$ ngẫu nhiên thuộc $a$, rồi kể từ bại liệt kẻ một đường thẳng liền mạch $b’$ qua $A$ và song song với $b$. Khi bại liệt $(\widehat {a,b}) = (\widehat {a,b’})$.
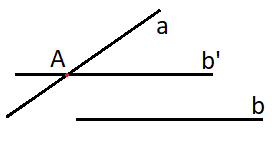
Xem thêm: 2m bằng bao nhiêu cm
Ví dụ 1: Cho hình chóp $S.ABCD$ với lòng là hình thoi cạnh $a$, $SA = a\sqrt 3 ,SA \bot BC$. Tính góc thân thích hai tuyến phố trực tiếp $SD$ và $BC$?
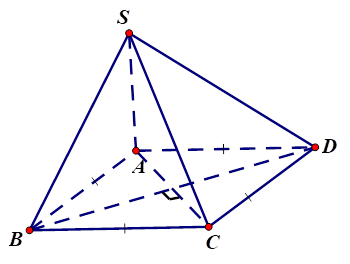
Ta có: $BC//AD.$
Do đó $(SD,BC) = (SD,AD) = \widehat {SDA}.$
Vì $\left. \begin{array}{l}
BC||AD\\
SA \bot BC
\end{array} \right\}$ $ \Rightarrow SA \bot AD \Rightarrow \widehat {SAD} = {90^0}.$
Xét tam giác $ΔSAD$ vuông bên trên $A$ tao có:
$\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \sqrt 3 $ $ \Rightarrow \widehat {SDA} = {60^0}.$
Vậy góc thân thích hai tuyến phố trực tiếp $SD$ và $BC$ vì như thế $60$ phỏng.
Ví dụ 2: Cho tứ diện $ABCD$ với $AB = CD = 2a$. Gọi $M, N$ thứu tự là trung điểm của $BC$ và $AD$, $MN = a\sqrt 3 $. Tính góc thân thích hai tuyến phố trực tiếp $AB$ và $CD$?

Xem thêm: trường đại học nguyễn trãi
Gọi $I$ là trung điểm của $BD.$
Ta có: $\left. \begin{array}{l}
IN//AB\\
IM//CD
\end{array} \right\}$ $ \Rightarrow (AB,CD) = (IM,IN).$
Xét tam giác $IMN$ có:
$IM = IN = a,MN = a\sqrt 3 .$
Do bại liệt $\cos \widehat {MIN} = \frac{{2{a^2} – 3{a^2}}}{{2{a^2}}} = – \frac{1}{2}$ $ \Rightarrow \widehat {MIN} = {120^0}.$
Vậy $(\widehat {AB,CD}) = {180^0} – {120^0} = {60^0}$.
Ví dụ 3: Cho hình lăng trụ $ABC.A’B’C’$ có tính nhiều năm cạnh mặt mày vì như thế $2a$, lòng $ABC$ là tam giác vuông bên trên $A$, $AB = a,AC = a\sqrt 3$. Hình chiếu vuông góc của $A’$ lên $mp(ABC)$ là trung điểm của $BC$. Tính $cosin$ của góc thân thích hai tuyến phố trực tiếp $AA’$ và $B’C’$?
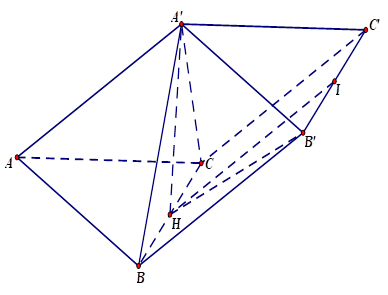
Gọi $H$ là trung điểm của $BC.$
Ta có: $\left. \begin{array}{l}
AA’//BB’\\
B’C’//BH
\end{array} \right\}$ $ \Rightarrow (AA’,B’C’) = (BB’,BH).$
Hay $\cos (AA’,B’C’) = \cos (BB’,BH)$ $ = \left| {\cos \widehat {HBB’}} \right|.$
Xét tam giác $A’B’H$ có:
$\widehat {A’} = {90^0},A’B’ = a.$
$A’H = \sqrt {AA{‘^2} – A{H^2}} $ $ = \sqrt {AA{‘^2} – {{\left( {\frac{{BC}}{2}} \right)}^2}} = a\sqrt 3 .$
Suy rời khỏi $HB’ = \sqrt {A'{H^2} + A’B{‘^2}} = 2a.$
Do đó $\cos \widehat {HBB’} = \frac{{B{H^2} + BB{‘^2} – HB{‘^2}}}{{2.BH.BB’}} = \frac{1}{4}.$
Vậy $\cos (AA’,B’C’) = \left| {\cos \widehat {HBB’}} \right| = \frac{1}{4}$.











Bình luận