Chủ đề tính bán kính đường tròn ngoại tiếp tam giác đều: Bán kính lối tròn xoe nước ngoài tiếp tam giác đều là 1 trong định nghĩa toán học tập thú vị và hữu ích. Đối với tam giác đều, bán kính đường tròn ngoại tiếp tam giác đều luôn luôn có mức giá trị thắt chặt và cố định, và việc đo lường và tính toán nó hỗ trợ chúng ta nắm rõ rộng lớn về cấu hình và tính chất đặc biệt quan trọng của tam giác đều. Tính bán kính đường tròn ngoại tiếp tam giác đều là 1 trong Việc thú vị và hữu ích vô giảng dạy dỗ và tiếp thu kiến thức toán học tập.
Công thức tính bán kính đường tròn ngoại tiếp tam giác đều là gì?
Công thức tính bán kính đường tròn ngoại tiếp tam giác đều là R = 2/3 * a, vô cơ R là nửa đường kính của lối tròn xoe nước ngoài tiếp tam giác đều và a là phỏng nhiều năm cạnh của tam giác đều.
Bạn đang xem: bán kính đường tròn ngoại tiếp tam giác đều

Định nghĩa về lối tròn xoe nước ngoài tiếp tam giác đều là gì?
Đường tròn xoe nước ngoài tiếp tam giác đều là 1 trong lối tròn xoe được vẽ sao cho tới trải qua những đỉnh của tam giác đều và đem tâm nằm tại trung điểm của những đoạn trực tiếp nối những đỉnh của tam giác. Bán kính của lối tròn xoe nước ngoài tiếp tam giác đều là khoảng cách kể từ tâm của lối tròn xoe cho tới ngẫu nhiên đỉnh này của tam giác. Đối với tam giác đều, lối tròn xoe nước ngoài tiếp đem nửa đường kính vì chưng 50% phỏng nhiều năm của một cạnh của tam giác.
Tại sao bán kính đường tròn ngoại tiếp tam giác đều được xem vì chưng một cạnh của tam giác?
Bán kính lối tròn xoe nước ngoài tiếp tam giác đều được xem vì chưng một cạnh của tam giác vì như thế vô tam giác đều, những cạnh và góc đều phải có độ quý hiếm như nhau. Đặt tam giác đều phải có cạnh vì chưng a. Khi vẽ lối tròn xoe nước ngoài tiếp tam giác đều, tao mang trong mình một lối tròn xoe trải qua những đỉnh của tam giác và lối tròn xoe này rời cạnh của tam giác tạo nên trở nên nhị phân giác đều. Do cơ, cạnh của tam giác rời lối tròn xoe nước ngoài tiếp trở nên nhị đoạn có tính nhiều năm đều bằng nhau. Vì vậy, nửa đường kính của lối tròn xoe nước ngoài tiếp tam giác đều được xem vì chưng một cạnh của tam giác.
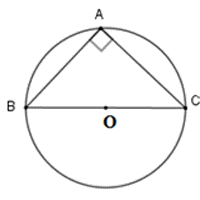
Cách tính bán kính đường tròn ngoại tiếp tam giác đều Toán lớp 10
Hãy coi Clip về bán kính đường tròn ngoại tiếp tam giác đều nhằm tìm hiểu một hướng nhìn mới mẻ vô học tập hình học tập. Quý khách hàng tiếp tục nắm rõ rộng lớn về phong thái đo lường và tính toán và phần mềm của nửa đường kính vô tam giác đều. Đây là Clip ko thể quăng quật qua!
Làm thế này nhằm tính bán kính đường tròn ngoại tiếp tam giác đều Khi chỉ biết phỏng nhiều năm một cạnh của tam giác?
Để tính bán kính đường tròn ngoại tiếp tam giác đều Khi chỉ biết phỏng nhiều năm một cạnh của tam giác, tao dùng công thức sau:
R = a / (2 * sin(π/3))
Trong cơ, R là bán kính đường tròn ngoại tiếp tam giác đều, a là phỏng nhiều năm một cạnh của tam giác.
Ví dụ, nếu như tao chỉ biết phỏng nhiều năm một cạnh của tam giác là 6cm, thì tao hoàn toàn có thể tính nửa đường kính lối tròn xoe nước ngoài tiếp như sau:
R = 6 / (2 * sin(π/3))
= 6 / (2 * √3 / 2)
= 6 / (2 * √3)
= 6 / (√3)
= 2√3 cm
Với a = 6cm, bán kính đường tròn ngoại tiếp tam giác đều là 2√3 centimet.
Làm thế này nhằm tính bán kính đường tròn ngoại tiếp tam giác đều lúc biết tọa phỏng của tía đỉnh tam giác?
Để tính bán kính đường tròn ngoại tiếp tam giác đều lúc biết tọa phỏng của tía đỉnh tam giác, tao hoàn toàn có thể tuân theo đuổi quá trình sau:
Bước 1: Xác ấn định tâm lối tròn xoe nước ngoài tiếp tam giác đều.
- Tìm tọa phỏng tâm lối tròn xoe nước ngoài tiếp tam giác đều bằng phương pháp lấy trung điểm của những đỉnh tam giác.
- Trước tiên, gọi tọa phỏng tía đỉnh tam giác thứu tự là A(x1, y1), B(x2, y2), và C(x3, y3).
- Lấy trung điểm của những đỉnh tam giác nhằm dò xét tọa phỏng tâm:
+ X = (x1 + x2 + x3)/3
+ Y = (y1 + y2 + y3)/3
- Tọa phỏng tâm lối tròn xoe nước ngoài tiếp tam giác đều là G(X, Y).
Bước 2: Tính khoảng cách kể từ tâm cho tới một đỉnh tam giác.
- Ta hoàn toàn có thể đo lường và tính toán khoảng cách kể từ tâm cho tới một đỉnh (ví dụ: đỉnh A) vì chưng công thức:
d = sqrt((x - x1)^2 + (y - y1)^2), với (x, y) là tọa phỏng tâm và (x1, y1) là tọa phỏng của đỉnh A.
Bước 3: Bán kính lối tròn xoe nước ngoài tiếp tam giác đều là khoảng cách kể từ tâm cho tới một đỉnh tam giác.
- Vì tam giác là tam giác đều, nên bán kính đường tròn ngoại tiếp tam giác đều tiếp tục vì chưng khoảng cách kể từ tâm cho tới một đỉnh tam giác, tức là bán kính đường tròn ngoại tiếp tam giác đều R = d.
Ví dụ: Giả sử tao đem tam giác đem tọa phỏng tía đỉnh là A(1, 2), B(4, 6), và C(7, 4). Ta cần thiết tính bán kính đường tròn ngoại tiếp tam giác đều.
Bước 1: Tính tọa phỏng tâm lối tròn xoe nước ngoài tiếp tam giác đều:
- X = (1 + 4 + 7)/3 = 4
- Y = (2 + 6 + 4)/3 = 4
=> Tọa phỏng tâm lối tròn xoe nước ngoài tiếp tam giác đều là G(4, 4).
Bước 2: Tính khoảng cách kể từ tâm cho tới một đỉnh tam giác:
- Ví dụ, nhằm tính khoảng cách kể từ tâm cho tới đỉnh A:
d = sqrt((4 - 1)^2 + (4 - 2)^2) = sqrt(9 + 4) = sqrt(13)
Bước 3: Bán kính lối tròn xoe nước ngoài tiếp tam giác đều là khoảng cách kể từ tâm cho tới một đỉnh tam giác:
- Vì tam giác là tam giác đều, nên bán kính đường tròn ngoại tiếp tam giác đều R = d = sqrt(13).
Do cơ, Khi tam giác đem tọa phỏng tía đỉnh là A(1, 2), B(4, 6), và C(7, 4), bán kính đường tròn ngoại tiếp tam giác đều là sqrt(13).

_HOOK_
Xem thêm: if parents bring up a child
Quy tắc này được dùng nhằm tính bán kính đường tròn ngoại tiếp tam giác đều vô hình học?
Quy tắc được dùng nhằm tính bán kính đường tròn ngoại tiếp tam giác đều vô hình học tập là quy tắc lối tròn xoe nước ngoài tiếp tam giác đều. Theo quy tắc này, nửa đường kính của lối tròn xoe nước ngoài tiếp tam giác đều tiếp tục vì chưng 50% phỏng nhiều năm cạnh của tam giác cơ.
Ví dụ, nếu như tao mang trong mình một tam giác đều với cạnh có tính nhiều năm là a, tao hoàn toàn có thể tính nửa đường kính của lối tròn xoe nước ngoài tiếp tam giác cơ vì chưng công thức R = a/2.
Đây là 1 trong quy tắc giản dị và đơn giản và dễ dàng dùng làm tính bán kính đường tròn ngoại tiếp tam giác đều vô hình học tập.
Tính nửa đường kính lối tròn xoe nội tiếp, nước ngoài tiếp tam giác
Muốn biết phương pháp lối tròn xoe hoàn toàn có thể nội tiếp hoặc nước ngoài tiếp tam giác? Xem Clip này nhằm dò xét hiểu cụ thể về nhị định nghĩa cần thiết này vô hình học tập. Chúng tiếp tục giúp cho bạn nắm rõ rộng lớn về quan hệ đằm thắm lối tròn xoe và tam giác.
Cách tính nửa đường kính hình tròn trụ nước ngoài tiếp tam giác Toán lớp 9 10
Bạn tiếp tục biết nửa đường kính của hình tròn trụ nước ngoài tiếp tam giác hoàn toàn có thể được xem toán thế nào không? Hãy nằm trong coi Clip nhằm dò xét hiểu về phong thái tính và phần mềm của nửa đường kính hình tròn trụ nước ngoài tiếp tam giác. Đây là kiến thức và kỹ năng hữu ích về hình học tập tuy nhiên các bạn tránh việc quăng quật lỡ!
Giải mến chân thành và ý nghĩa của bán kính đường tròn ngoại tiếp tam giác đều vô quy trình xử lý những Việc hình học?
Bán kính lối tròn xoe nước ngoài tiếp tam giác đều là độ quý hiếm nửa đường kính của một lối tròn xoe đem tâm là tâm tam giác đều và trải qua tía đỉnh của tam giác. Đây là 1 trong đại lượng cần thiết vô quy trình xử lý những Việc hình học tập tương quan cho tới tam giác đều.
Ý nghĩa của bán kính đường tròn ngoại tiếp tam giác đều là:
1. Hình trở nên lối tròn xoe nước ngoài tiếp: Bán kính này canh ty xác lập được lối tròn xoe nước ngoài tiếp tam giác đều, tạo nên trở nên một lối tròn xoe chứa chấp cả tam giác và đem tâm là tâm tam giác. Đường tròn xoe này còn có tầm quan trọng cần thiết trong các công việc tế bào phỏng, đo lường và tính toán và đánh giá những tính chất của tam giác đều.
2. Kết nối trong số những đỉnh của tam giác: Bán kính lối tròn xoe nước ngoài tiếp tam giác đều liên kết những đỉnh của tam giác lại cùng nhau trải qua một lối tròn xoe có một không hai. Vấn đề này đưa đến một côn trùng link đặc biệt quan trọng và đồng đều trong số những thành phần của tam giác, canh ty đơn giản nhận ra và vận dụng những đặc thù tam giác đều vô quy trình xử lý Việc.
3. Hỗ trợ vô đo lường và tính toán và phân tách hình học: Giá trị bán kính đường tròn ngoại tiếp tam giác đều được dùng nhằm đo lường và tính toán diện tích S, chu vi, cung, tiếp tuyến và những thông số kỹ thuật không giống của tam giác. Nó hỗ trợ một hạ tầng toán học tập chắc hẳn rằng nhằm xác lập những tính chất và quy luật tương quan cho tới tam giác đều, kể từ cơ xử lý những Việc hình học tập phức tạp rộng lớn.
Trong tổ hợp, bán kính đường tròn ngoại tiếp tam giác đều đem tầm quan trọng cần thiết trong các công việc xác lập và vận dụng những đặc thù của tam giác đều và đưa đến côn trùng link trong số những đỉnh của tam giác. Nó vào vai trò cần thiết vô quy trình xử lý những Việc hình học tập và phân tách hình học tập của tam giác.

Trình bày ví dụ rõ ràng về sự tính bán kính đường tròn ngoại tiếp tam giác đều vô một Việc hình học tập.
Ví dụ rõ ràng về sự tính bán kính đường tròn ngoại tiếp tam giác đều vô một Việc hình học tập như sau:
Giả sử tất cả chúng ta mang trong mình một tam giác đều ABC với phỏng nhiều năm cạnh vì chưng a. Chúng tao cần thiết tính nửa đường kính lối tròn xoe nước ngoài tiếp tam giác này.
Bước 1: Tìm lối trung trực của một cạnh của tam giác. Đường trung trực là đường thẳng liền mạch trải qua trung điểm của cạnh và vuông góc với cạnh cơ. Trong tình huống này, tất cả chúng ta hoàn toàn có thể lựa chọn cạnh AB thực hiện ví dụ.
Bước 2: Xác ấn định tâm O của lối tròn xoe nước ngoài tiếp tam giác. Để thực hiện điều này, tao cần thiết dò xét phú điểm của hai tuyến đường trung trực. Trong tình huống này, tất cả chúng ta cần thiết dò xét phú điểm của lối trung trực của cạnh AB và lối trung trực của cạnh AC. Điểm phú điểm đó đó là tâm O của lối tròn xoe nước ngoài tiếp tam giác ABC.
Bước 3: Xác ấn định nửa đường kính của lối tròn xoe nước ngoài tiếp. Để thực hiện điều này, tất cả chúng ta cần thiết tính phỏng nhiều năm của quãng lối OA (hoặc OB hoặc OC). Bán kính R của lối tròn xoe nước ngoài tiếp tam giác ABC đó là phỏng nhiều năm AO (hoặc BO hoặc CO).
Bước 4: sát dụng công thức tính nửa đường kính. Với tam giác đều ABC, phỏng nhiều năm cạnh a tiếp tục nghĩ rằng biết. Theo công thức, nửa đường kính R của lối tròn xoe nước ngoài tiếp tam giác đều là:
R = a/(2*sqrt(3))
Ví dụ, nếu như tao đem tam giác đều ABC với cạnh a = 9 centimet, tao hoàn toàn có thể tính nửa đường kính R bằng phương pháp thay cho vô công thức:
R = 9/(2*sqrt(3)) ≈ 3.27 cm
Vậy bán kính đường tròn ngoại tiếp tam giác đều ABC có tính nhiều năm khoảng tầm 3.27 centimet.
Làm sao nhằm minh chứng rằng một lối tròn xoe là lối tròn xoe nước ngoài tiếp tam giác đều?
Để minh chứng rằng một lối tròn xoe là lối tròn xoe nước ngoài tiếp tam giác đều, tao cần thiết triển khai quá trình sau đây:
Bước 1: Vẽ tam giác đều ABC với những cạnh đồng nhiều năm và những góc đều bằng nhau.
Bước 2: Vẽ lối tròn xoe nước ngoài tiếp tam giác gọi là là (O) và xác lập tâm lối tròn xoe là O.
Bước 3: Khi tao đem tam giác đều ABC, tao hiểu được tâm lối tròn xoe nước ngoài tiếp tam giác đều ở vô trọng tâm G và trung điểm của những đỉnh của tam giác. Vì vậy, tao cần thiết minh chứng rằng G và O là và một điểm.
Bước 4: Ta hiểu được trọng tâm G là vấn đề trung điểm của những đỉnh tam giác và tâm lối tròn xoe nước ngoài tiếp tam giác đều. Do cơ, tao cần thiết minh chứng rằng G và O là và một điểm.
Bước 5: Để minh chứng rằng G và O là và một điểm, tao hoàn toàn có thể dùng đặc thù của tam giác đều. Vì những cạnh tam giác đều đồng nhiều năm và những góc đều đều bằng nhau, tao hoàn toàn có thể minh chứng rằng G và O cơ hội những đỉnh tam giác một khoảng tầm đều bằng nhau.
Bước 6: Với quá trình bên trên, tao tiếp tục minh chứng rằng G và O là và một điểm và vì thế lối tròn xoe nước ngoài tiếp tam giác đem tâm là G cũng chính là lối tròn xoe nước ngoài tiếp tam giác đều.
Xem thêm: đề thi cấp 3 năm 2022

Tìm hiểu về phần mềm của tính bán kính đường tròn ngoại tiếp tam giác đều vô thực tiễn.
Trong thực tiễn, tính bán kính đường tròn ngoại tiếp tam giác đều đem phần mềm cần thiết trong không ít nghành nghề dịch vụ. Dưới đấy là một vài phần mềm thông dụng của việc đo lường và tính toán bán kính đường tròn ngoại tiếp tam giác đều:
1. Xây dựng công trình: Khi thiết kế những dự án công trình, như cầu, tòa căn nhà, hầm đường đi bộ, việc đo lường và tính toán bán kính đường tròn ngoại tiếp tam giác đều canh ty xác lập độ cao thấp và hình dạng của những đài phun nước, cột đèn, vòng tròn xoe và những cạnh lối tròn xoe nước ngoài tiếp tam giác.
2. Thiết tiếp vật dụng họa: Trong kiến thiết hình họa, việc tính bán kính đường tròn ngoại tiếp tam giác đều canh ty đưa đến hình hình ảnh đẹp mắt và bằng vận. Nó được dùng trong các công việc kiến thiết logo, hình tượng, thẩm mỹ và nghệ thuật và những kiến thiết không giống muốn tạo rời khỏi những hình dạng đẹp mắt và hài hòa và hợp lý.
3. Địa hóa học học: Trong phân tích địa hóa học, tính bán kính đường tròn ngoại tiếp tam giác đều hoàn toàn có thể được dùng nhằm xác lập độ cao thấp và hình dạng của những vùng núi và hố sụt. Nó cũng hoàn toàn có thể canh ty trong các công việc đưa đến quy mô địa hóa học và Dự kiến những hiện tượng kỳ lạ ngẫu nhiên.
4. Điều khiển tự động động: Trong technology điều khiển và tinh chỉnh tự động hóa, đo lường và tính toán bán kính đường tròn ngoại tiếp tam giác đều hoàn toàn có thể được dùng nhằm xác lập khoảng cách và địa điểm trong số những đối tượng người dùng vô khối hệ thống.
5. Kỹ thuật xây dựng: Trong ngành chuyên môn thiết kế, đo lường và tính toán bán kính đường tròn ngoại tiếp tam giác đều hoàn toàn có thể được dùng nhằm xác xác định trí và độ cao thấp của những kết cấu, như bậc lan can, trái khoáy cầu tô điểm, nón đèn, v.v.
Tính bán kính đường tròn ngoại tiếp tam giác đều là 1 trong cách thức cần thiết và hữu ích trong các công việc xử lý những yếu tố thực tiễn trong không ít nghành nghề dịch vụ không giống nhau.
_HOOK_













Bình luận