cách chứng minh vuông góc

Để chứng tỏ hai tuyến đường trực tiếp là vuông góc vô hình học tập lớp 7, tất cả chúng ta hoàn toàn có thể dùng một trong những cách thức sau đây:
Phương pháp 1: Sử dụng quyết định nghĩa
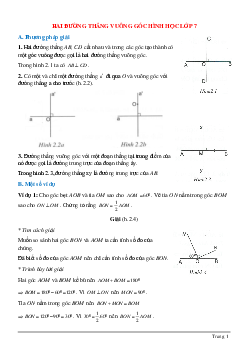
Theo khái niệm, hai tuyến đường trực tiếp được gọi là vuông góc nếu như phú nhau tạo ra trở nên 4 góc vuông (mỗi góc vì thế 90 độ). Để chứng tỏ hai tuyến đường trực tiếp là vuông góc, tớ hoàn toàn có thể tuân theo quá trình sau:
Bước 1: Vẽ hai tuyến đường trực tiếp cần thiết đánh giá.
Bước 2: Sử dụng thước đo góc hoặc khí cụ nhằm đo góc bên trên nút giao nhau của hai tuyến đường trực tiếp.
Bước 3: Nếu cả 4 góc đo được đều vì thế 90 phỏng, thì hai tuyến đường trực tiếp này đó là vuông góc. trái lại, nếu như tối thiểu một trong những số 4 góc ko vì thế 90 phỏng, hai tuyến đường trực tiếp ko vuông góc.
Phương pháp 2: Sử dụng tích hóa học của những đường thẳng liền mạch vuông góc
Có một trong những tích hóa học của những đường thẳng liền mạch vuông góc tuy nhiên tất cả chúng ta hoàn toàn có thể dùng nhằm chứng tỏ tính vuông góc của hai tuyến đường trực tiếp. Một số vô số ê là:
- Tích hóa học 1: Đường trực tiếp tuy nhiên song với 1 đường thẳng liền mạch vuông góc với đường thẳng liền mạch không giống cũng chính là vuông góc với đường thẳng liền mạch ê.
- Tích hóa học 2: Trong một tam giác vuông, lối cao cạnh huyền là đường thẳng liền mạch vuông góc đối với tất cả nhị cạnh góc vuông.
- Tích hóa học 3: Nếu đường thẳng liền mạch AB vuông góc với đường thẳng liền mạch CD và cả đường thẳng liền mạch CD và DE tuy nhiên song với đường thẳng liền mạch AE, thì BM tiếp tục vuông góc với AE.
Chúng tớ hoàn toàn có thể dùng những đặc thù bên trên nhằm chứng tỏ tính vuông góc của hai tuyến đường trực tiếp vô một việc rõ ràng.
Lưu ý rằng, nhằm chứng tỏ hai tuyến đường trực tiếp là vuông góc, tớ nên dùng cả nhị cách thức bên trên hoặc dùng những cách thức không giống phù phù hợp với từng việc rõ ràng.

Bạn đang xem: cách chứng minh vuông góc

Hai đường thẳng liền mạch vuông góc là hai tuyến đường trực tiếp tuy nhiên phú nhau tạo ra trở nên một góc vuông, tức là góc có tính rộng lớn vì thế 90 phỏng. Để chứng tỏ hai tuyến đường trực tiếp vuông góc, tớ cần thiết xác lập rằng những đường thẳng liền mạch ê phú nhau và góc thân thiện bọn chúng là góc vuông.
Có một trong những cách thức chứng tỏ hai tuyến đường trực tiếp vuông góc, như chứng tỏ dùng đặc thù của những đường thẳng liền mạch tuy nhiên song hoặc dùng những cách thức hình học tập không giống. Dưới đó là một cách thức chứng tỏ trải qua đặc thù của lối cao vô tam giác:
Giả sử tớ với hai tuyến đường trực tiếp AB và CD. Để chứng tỏ bọn chúng vuông góc nhau, tớ tổ chức quá trình sau:
1. Vẽ một điểm E bên trên đường thẳng liền mạch CD.
2. Vẽ đường thẳng liền mạch đứng AH vuông góc với đường thẳng liền mạch CD bên trên điểm E.
3. Nếu tớ chứng tỏ được AB tuy nhiên song với đường thẳng liền mạch AH, thì tớ hoàn toàn có thể Kết luận rằng AB vuông góc với CD.
4. Để chứng tỏ AB tuy nhiên song với AH, tớ cần thiết chứng tỏ góc AHB là góc nhọn (góc nhọn là góc có tính rộng lớn nhỏ rộng lớn 90 độ) hoặc góc AHB là góc tù (góc tù là góc có tính rộng lớn to hơn 90 độ).
5. Nếu góc AHB là góc nhọn hoặc góc tù, thì AB sẽ không còn rời AH và vì thế AB tiếp tục tuy nhiên song với AH.
6. Vì AB tuy nhiên song với AH, và AH vuông góc với CD bên trên điểm E, nên tớ hoàn toàn có thể Kết luận rằng AB vuông góc với CD.
Qua quy trình chứng tỏ bên trên, tớ vẫn chứng tỏ được hai tuyến đường trực tiếp AB và CD là vuông góc nhau. Từ ê, tớ hoàn toàn có thể khái niệm hai tuyến đường trực tiếp vuông góc là hai tuyến đường trực tiếp tuy nhiên phú nhau tạo ra trở nên một góc vuông, tức là góc có tính rộng lớn vì thế 90 phỏng.

Để chứng tỏ hai tuyến đường trực tiếp vuông góc cùng nhau vô hình học tập lớp 7, tất cả chúng ta hoàn toàn có thể vận dụng một trong những nguyên tắc sau:
1. Nguyên lý góc vuông: Xét hai tuyến đường trực tiếp AB và CD. Để chứng tỏ rằng bọn chúng vuông góc cùng nhau, tớ cần thiết chứng tỏ rằng góc thân thiện hai tuyến đường này là góc vuông. Cụ thể, tất cả chúng ta cần thiết chứng tỏ rằng AB và CD tạo ra trở nên 1 cặp góc vì thế 90 phỏng (góc vuông). Để thực hiện điều này, hoàn toàn có thể dùng những theorem về góc cùng nhau, ví như góc nội tiếp, góc chéo cánh tạo ra vì thế hai tuyến đường chéo cánh vô hình vuông vắn, hoặc những theorem về góc ông xã lên nhau.
2. Nguyên lý đường thẳng liền mạch vuông góc và đường thẳng liền mạch tuy nhiên song: Xét hai tuyến đường trực tiếp AB và CD. Để chứng tỏ rằng bọn chúng vuông góc cùng nhau, tớ cần thiết chứng tỏ rằng bọn chúng ko tuy nhiên song và tồn bên trên một đường thẳng liền mạch EF rời AB và CD bên trên nhị điểm E và F sao cho những góc được tạo ra trở nên vì thế những đoạn trực tiếp AE, EF và FC là góc vuông. Để thực hiện điều này, hoàn toàn có thể dùng những theorem về phú điểm thân thiện hai tuyến đường trực tiếp hoặc cơ hội chứng tỏ đường thẳng liền mạch tuy nhiên song và đường thẳng liền mạch vuông góc vô hình học tập.
Lưu ý: Để chứng tỏ hai tuyến đường trực tiếp vuông góc vô hình học tập, tất cả chúng ta cần thiết nhờ vào những nguyên tắc và theorem vẫn học tập vô lớp 7. Việc thể hiện được cơ hội chứng tỏ rõ ràng đòi hỏi nghiên cứu và phân tích tăng và lần hiểu những việc và theorem tương quan.

Để hai tuyến đường trực tiếp được xem là vuông góc, cần thiết thỏa mãn nhu cầu một trong những ĐK sau:
1. Đường trực tiếp cần rời nhau, tức là ko tuy nhiên song cùng nhau.
2. Góc thân thiện hai tuyến đường trực tiếp rời cần là góc vuông, tức là đạt được được 90 phỏng.
Điều khiếu nại này hoàn toàn có thể được thể hiện tại vì thế phương trình hoặc công thức, tùy nằm trong vô cách thức chứng tỏ dùng.
Ví dụ:
- Nếu với hai tuyến đường trực tiếp thực hiện vì thế những phương trình với thông số góc không giống nhau, tớ cần thiết chứng tỏ rằng tích của nhị thông số góc này cần vì thế -1 nhằm chứng tỏ hai tuyến đường trực tiếp vuông góc.
- Nếu với hai tuyến đường trực tiếp được trình diễn bên dưới dạng vector, tớ cần thiết chứng tỏ rằng tích vô vị trí hướng của nhị vector này cần vì thế 0 nhằm chứng tỏ hai tuyến đường trực tiếp vuông góc.
Với từng cách thức chứng tỏ, cần thiết vận dụng công thức ứng và chứng tỏ rằng đường thẳng liền mạch thỏa mãn nhu cầu ĐK bên trên.

Để đánh giá coi hai tuyến đường trực tiếp với vuông góc cùng nhau hay là không, tớ triển khai quá trình sau đây:
Bước 1: Tìm thông số góc của hai tuyến đường trực tiếp. Gọi thông số góc của đường thẳng liền mạch loại nhất là m1 và đường thẳng liền mạch loại nhị là mét vuông.
Bước 2: Sử dụng công thức tính thông số góc của lối thẳng:
m = (y2 - y1) / (x2 - x1)
Bước 3: Tính tích của nhị thông số góc m1 * mét vuông. Nếu tích này vì thế -1, tức là hai tuyến đường trực tiếp là vuông góc cùng nhau.
Ví dụ:
Cho hai tuyến đường trực tiếp với phương trình:
Đường trực tiếp 1: hắn = 3x + 2
Đường trực tiếp 2: hắn = -1/3x + 5
Bước 1: Hệ số góc của đường thẳng liền mạch một là m1 = 3 và đường thẳng liền mạch 2 là mét vuông = -1/3.
Bước 2: Tính tích m1 * mét vuông = 3 * (-1/3) = -1.
Bước 3: Vì tích m1 * mét vuông = -1, nên hai tuyến đường trực tiếp vẫn nghĩ rằng vuông góc cùng nhau.
Vậy này đó là cơ hội đánh giá coi hai tuyến đường trực tiếp với vuông góc cùng nhau hay là không.

7 là:
- Định nghĩa: Hai đường thẳng liền mạch gọi là vuông góc Lúc tổng nhị góc vì thế 90 phỏng.
- Tính hóa học 1: Hai đường thẳng liền mạch vuông góc sẽ tạo nên trở nên tư góc vuông cân nhau.
- Tính hóa học 2: Đường cao của tam giác vuông cũng chính là lối vuông góc với cạnh huyền của tam giác.
- Tính hóa học 3: Điểm công cộng của hai tuyến đường trực tiếp vuông góc được xem là trung điểm của đoạn trực tiếp nối nhị điểm chân của lối cao.
- Tính hóa học 4: Nếu với hai tuyến đường trực tiếp rời nhau bên trên một điểm và tạo ra trở nên nhị góc đồng đều, thì hai tuyến đường trực tiếp này đó là vuông góc.

Để lần đường thẳng liền mạch vuông góc trải qua một điểm bên trên đường thẳng liền mạch vẫn biết, tớ hoàn toàn có thể tuân theo quá trình sau đây:
Bước 1: Xác quyết định đường thẳng liền mạch vẫn biết và điểm bên trên đường thẳng liền mạch cần thiết trải qua.
- Định rõ ràng đường thẳng liền mạch vẫn biết, ví dụ: hắn = mx + c, vô ê m là phỏng dốc của đường thẳng liền mạch và c là thông số phú với trục hắn.
- Chọn vấn đề cần trải qua bên trên đường thẳng liền mạch vẫn biết, trải qua tọa phỏng của chính nó, ví dụ (x₁, y₁).
Bước 2: Tìm đường thẳng liền mạch vuông góc.
- Đường trực tiếp vuông góc trải qua một điểm x₁, y₁ bên trên đường thẳng liền mạch vẫn biết với Đặc điểm là phỏng dốc nghịch ngợm hòn đảo và trái khoáy vệt đối với đường thẳng liền mạch vẫn biết.
- Độ dốc của đường thẳng liền mạch vuông góc là -1/m, tức thị nghịch ngợm hòn đảo của phỏng dốc m của đường thẳng liền mạch vẫn biết.
- Từ ê, tớ với bộ phận đường thẳng liền mạch vuông góc là hắn = (−1/m)x + b, vô ê b là thông số phú với trục hắn.
Bước 3: Xác quyết định thông số phú điểm.
- Để xác lập thông số phú điểm b của đường thẳng liền mạch vuông góc, tớ dùng vấn đề về điểm vẫn lựa chọn (x₁, y₁) bên trên đường thẳng liền mạch vẫn biết.
- Thế tọa phỏng của điểm vẫn lựa chọn vô phương trình hắn = (−1/m)x + b, tớ với y₁ = (−1/m)x₁ + b.
- Từ ê, tớ hoàn toàn có thể tính được thông số phú điểm b = y₁ + (1/m)x₁.
Sau Lúc tuân theo quá trình bên trên, tớ tiếp tục tìm kiếm ra phương trình của đường thẳng liền mạch vuông góc trải qua điểm vẫn lựa chọn bên trên đường thẳng liền mạch vẫn biết.

Để chứng tỏ đường thẳng liền mạch tạo ra góc 90 phỏng với một phía phẳng phiu là đường thẳng liền mạch vuông góc với mặt mày phẳng phiu ê, tất cả chúng ta hoàn toàn có thể vận dụng cách thức dùng tích vô phía (dot product) của nhị vector.
Với một phía phẳng phiu vẫn mang lại và một đường thẳng liền mạch ko phía trên mặt mày phẳng phiu ê, tớ lựa chọn nhị vector a và b. Vector a xuôi theo đường thẳng liền mạch và vector b chạy vuông góc với mặt mày phẳng phiu.
Bước 1: Tạo vector a đi đường trực tiếp bằng phương pháp lựa chọn nhị điểm bên trên đường thẳng liền mạch và tính hiệu của những tọa phỏng của nhị điểm ê. Ví dụ, fake sử nhị điểm bên trên đường thẳng liền mạch thứu tự là A(x1, y1, z1) và B(x2, y2, z2). Ta xây đắp vector a = AB = (x2 - x1, y2 - y1, z2 - z1).
Bước 2: Xác quyết định vector pháp tuyến của mặt mày phẳng phiu vẫn mang lại. Vector này hoàn toàn có thể được lần bằng phương pháp lựa chọn tía điểm nằm trong mặt mày phẳng phiu và tính vector pháp tuyến vì thế tích chéo cánh (cross product) của nhị vector chỉ phần tọa phỏng ứng của tía điểm ê.
Bước 3: Tính tích vô vị trí hướng của nhị vector a và vector pháp tuyến của mặt mày phẳng phiu bằng phương pháp nhân từng thành phần ứng của nhị vector cùng nhau, rồi với những thành phẩm. Nếu tích vô phía này vì thế 0, tức là nhị vector vuông góc cùng nhau và vì thế đường thẳng liền mạch tạo ra góc 90 phỏng với mặt mày phẳng phiu.
Như vậy, nếu như tớ triển khai những bước bên trên và thành phẩm tích vô phía vì thế 0, tất cả chúng ta hoàn toàn có thể chứng tỏ được đường thẳng liền mạch tạo ra góc 90 phỏng với mặt mày phẳng phiu là đường thẳng liền mạch vuông góc với mặt mày phẳng phiu ê.

Để chứng tỏ sự tồn bên trên của hai tuyến đường trực tiếp vuông góc vô không khí tía chiều, tớ hoàn toàn có thể dùng cách thức dùng vectơ và tích vô phía.
Giả sử hai tuyến đường trực tiếp là đường thẳng liền mạch d1 và d2. Để chứng tỏ bọn chúng vuông góc nhau, tớ cần thiết chứng tỏ rằng vectơ vị trí hướng của d1 và vectơ vị trí hướng của d2 với tích vô phía vì thế 0.
Bước 1: Gọi vectơ vị trí hướng của đường thẳng liền mạch d1 là vector1(a1, b1, c1) và vectơ vị trí hướng của đường thẳng liền mạch d2 là vector2(a2, b2, c2).
Bước 2: Tính tích vô phía thân thiện vector1 và vector2 vì thế công thức:
a = a1 * a2 + b1 * b2 + c1 * c2.
Bước 3: Kiểm tra độ quý hiếm của a. Nếu a = 0, tức là tích vô phía vì thế 0, thì tớ hoàn toàn có thể Kết luận đường thẳng liền mạch d1 và d2 là vuông góc nhau. trái lại, nếu như a không giống 0, tớ ko thể Kết luận hai tuyến đường trực tiếp vuông góc.
Đây là cơ hội chứng tỏ sự tồn bên trên của hai tuyến đường trực tiếp vuông góc vô không khí tía chiều vì thế cách thức dùng vectơ và tích vô phía. Tuy nhiên, cơ hội chứng tỏ này hoàn toàn có thể chỉ vận dụng được vô một trong những tình huống, và còn thật nhiều cách thức không giống nhằm chứng tỏ sự tồn bên trên của hai tuyến đường trực tiếp vuông góc.

Xem thêm: văn tả cái cặp lớp 5

Đường trực tiếp vuông góc là một trong định nghĩa cần thiết vô hình học tập và có không ít phần mềm vô cuộc sống hằng ngày và những nghành nghề không giống. Dưới đó là một trong những phần mềm cơ bạn dạng của đường thẳng liền mạch vuông góc:
1. Xây dựng và loài kiến trúc: Trong nghành nghề xây đắp và bản vẽ xây dựng, một đường thẳng liền mạch vuông góc được dùng nhằm xác lập những góc vuông và phân loại không khí trở nên những chống, những tầng và những điểm không giống nhau. Như vậy hùn tăng tính tiện lợi và bố trí phù hợp vô công trình xây dựng xây đắp.
2. Thương mại và phú thông: Đường trực tiếp vuông góc được dùng thật nhiều vô nghành nghề kinh doanh và giao thông vận tải. Ví dụ, trong các việc xây đắp những tòa căn nhà nhà ở, cần thiết xác lập những lối phân loại nhằm tận dụng tối đa không khí một cơ hội hiệu suất cao. Trên trên phố, những góc vuông được dùng nhằm xác lập quang cảnh giao thông vận tải, đáp ứng sự tin cậy và thuận tiện cho những người lên đường lối.
3. Địa lý và bạn dạng đồ: Trong nghành nghề địa lý và bạn dạng vật, đường thẳng liền mạch vuông góc được dùng nhằm xác lập những góc và phía, hùn xác định và tính toán địa lý đúng chuẩn. Việc dùng đường thẳng liền mạch vuông góc vô công tác làm việc bạn dạng vật cũng hùn đáp ứng tính đúng chuẩn và tiện nghi của bạn dạng vật.
4. Kỹ thuật và công nghệ: Trong nghành nghề chuyên môn và technology, đường thẳng liền mạch vuông góc được dùng nhằm xác lập những phía và địa điểm, hùn design và xây đắp những thành phầm đúng chuẩn. Ví dụ, trong các việc lắp đặt ráp những thành phần công cụ, những đường thẳng liền mạch vuông góc được dùng nhằm xác xác định trí đúng chuẩn của từng thành phần.
5. Trong toán học tập và hình học: Đường trực tiếp vuông góc là một trong định nghĩa cơ bạn dạng vô toán học tập và được dùng trong không ít việc và cách thức chứng tỏ không giống nhau. Việc hiểu và vận dụng những công thức và quy tắc của đường thẳng liền mạch vuông góc hùn xử lý những việc phức tạp vô toán học tập và hình học tập.
Đường trực tiếp vuông góc không chỉ có với phần mềm vô hình học tập mà còn phải trong không ít nghành nghề không giống nhau vô cuộc sống hằng ngày. Hiểu và phần mềm đường thẳng liền mạch vuông góc là một trong khả năng cần thiết nhằm xử lý những yếu tố thực tiễn và cải cách và phát triển trí tuệ.