công thức tính đường trung tuyến

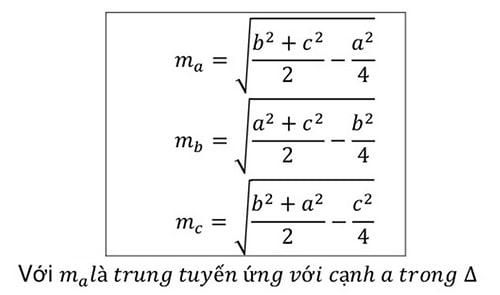
Công thức tính chừng nhiều năm đàng trung tuyến nhập tam giác là căn bậc nhì của 1 phần 2 tổng bình phương nhì cạnh kề. Trước hết, tất cả chúng ta tiếp tục lần trung điểm của cạnh cần thiết tính chừng nhiều năm đàng trung tuyến. Sau cơ, tính chừng nhiều năm cạnh đối lập với cạnh tất cả chúng ta đang được tìm ra trung điểm. Tiếp theo gót, bình phương chừng nhiều năm nhì cạnh kề của cạnh tất cả chúng ta đang được lần và nằm trong lại. Tiếp theo gót, lấy 1 phần 2 tổng bình phương nhì cạnh kề. Cuối nằm trong, lấy căn bậc nhì của thành phẩm nhằm tính chừng nhiều năm đàng trung tuyến.

Bạn đang xem: công thức tính đường trung tuyến

Để tính chừng nhiều năm đàng trung tuyến nhập tam giác cân nặng, tao dùng công thức sau:
Độ nhiều năm đàng trung tuyến = căn bậc 2 của 1 phần 2 tổng bình phương nhì cạnh kề trừ lên đường 1 phần tư bình phương cạnh đối.
Ví dụ, fake sử nhập tam giác ABC, tao có tính nhiều năm cạnh AB = 10 centimet và cạnh AC = 10 centimet. Cách thứ nhất, tao tính tổng bình phương nhì cạnh kề:
Tổng bình phương nhì cạnh kề = AB^2 + AC^2 = 10^2 + 10^2 = 200.
Tiếp theo gót, tao tính 1 phần nhì của tổng bình phương nhì cạnh kề:
Một phần 2 tổng bình phương nhì cạnh kề = một nửa * 200 = 100.
Sau cơ, tao tính bình phương cạnh đối:
Bình phương cạnh đối = BC^2 = 12^2 = 144.
Cuối nằm trong, tao tính 1 phần tư bình phương cạnh đối:
Một phần tư bình phương cạnh đối = 1/4 * 144 = 36.
Tiếp theo gót, tao trừ 1 phần tư bình phương cạnh đối kể từ 1 phần 2 tổng bình phương nhì cạnh kề:
Độ nhiều năm đàng trung tuyến = căn bậc 2 của (100 - 36) = căn bậc 2 của 64 = 8 centimet.
Vì vậy, nhập tam giác ABC cân nặng với cạnh AB = 10 centimet và cạnh AC = 10 centimet, chừng nhiều năm đàng trung tuyến là 8 centimet.

Để tính chừng nhiều năm đàng trung tuyến nhập tam giác cân nặng, tao hoàn toàn có thể vận dụng công thức sau:
- Để lần chừng nhiều năm đàng trung tuyến loại i, tao dùng công thức sau: Tường dạng: giờ việt C.
Đầu tiên, tao xác lập chừng nhiều năm cạnh cân nặng là a.
Tiếp theo gót, tao lần trung điểm M của cạnh cân nặng cơ. Với tam giác cân nặng, trung điểm của cạnh cân nặng trùng khớp với tâm của đàng trung trực trải qua nó.
Sau cơ, tao dùng công thức chừng nhiều năm đàng trung tuyến as nhập binh phương của hạch sách cạnh vì chưng nửa tổng của những binh phương của nhì cạnh kề.
Vì tam giác cân nặng sở hữu nhì cạnh kề đều bằng nhau, nên công thức bên trên cũng giản dị hơn: chừng nhiều năm đàng trung tuyến nhập tam giác cân đối 50% chừng nhiều năm cạnh cân nặng.
Ví dụ:
Giả sử tao sở hữu một tam giác cân nặng với cạnh cân nặng có tính nhiều năm là 10 centimet. Ta cần thiết tính chừng nhiều năm đàng trung tuyến nhập tam giác này.
Bước 1: Xác quyết định cạnh cân nặng là a = 10 centimet.
Bước 2: Tìm trung điểm M của cạnh cân nặng. Với tam giác cân nặng, trung điểm cạnh cân nặng trùng với tâm đàng trung trực trải qua cạnh cân nặng. Do cơ, trung điểm M nằm tại thân mật cạnh cân nặng và có tính nhiều năm là 10/2 = 5 centimet.
Bước 3: Sử dụng công thức chừng nhiều năm đàng trung tuyến, tao có: chừng nhiều năm đàng trung tuyến = 5 centimet.
Vậy, chừng nhiều năm đàng trung tuyến nhập tam giác cân nặng sở hữu cạnh cân nặng là 10 centimet là 5 centimet.

Công thức căn bậc nhì được dùng nhằm tính chừng nhiều năm đàng trung tuyến vì thế nó dựa vào đặc thù của tam giác cân nặng.
Trong một tam giác cân nặng, đàng trung tuyến là đoạn trực tiếp nối một đỉnh cho tới trung điểm của cạnh đối lập. Như vậy, tao sở hữu hai tuyến đường trung tuyến cho tới nhì cạnh kề và một đàng trung tuyến cho tới cạnh đối.
Để tính chừng nhiều năm đàng trung tuyến, tao dùng công thức căn bậc nhì như sau:
1. Tính tổng bình phương của nhì cạnh kề:
Tính tổng bình phương của nhì cạnh kề (AB và AC) và thành phẩm được gọi là tổng bình phương nhì cạnh kề (AB^2 + AC^2).
2. Lấy 50% của tổng bình phương nhì cạnh kề:
Chia tổng bình phương nhì cạnh kề cho tới 2 và thành phẩm tiếp tục là 1 trong những nửa của tổng bình phương nhì cạnh kề.
3. Lấy căn bậc nhì của 50% tổng bình phương nhì cạnh kề:
Áp dụng công thức căn bậc nhì nhằm lấy căn bậc nhì của 50% tổng bình phương nhì cạnh kề. Kết ngược đó là chừng nhiều năm đàng trung tuyến.
Sử dụng công thức căn bậc nhì nhằm tính chừng nhiều năm đàng trung tuyến hùn tất cả chúng ta hoàn toàn có thể lần rời khỏi thành phẩm đúng chuẩn và nhanh gọn lẹ dựa vào vấn đề về cạnh của tam giác cân nặng.

Đường trung tuyến của tam giác cân nặng luôn luôn có tính nhiều năm đều bằng nhau. Để chứng tỏ điều này, tao xét tam giác ABC cân nặng bên trên đỉnh A. Gọi M là trung điểm của cạnh BC. Khi cơ, đàng trung tuyến AM đó là đàng trọng tâm và rời BM bên trên điểm G sao cho tới MG = 2GM.
Chứng minh: Ta thấy tam giác BMG là tam giác vuông bên trên G (BM là đàng cao của tam giác ABC). sít dụng quyết định lý Pythagoras cho tới tam giác BMG, tao có:
BG² = BM² - GM²
Trong tam giác cân nặng ABC, tao sở hữu AB = AC. Do cơ, AM cũng chính là đàng cao của tam giác ABC và như thế AM = GM.
Từ cơ, tao suy rời khỏi rằng đàng trung tuyến AM của tam giác cân nặng ABC có tính nhiều năm đều bằng nhau với BM và CM, tức là đàng trung tuyến của tam giác cân nặng luôn luôn có tính nhiều năm đều bằng nhau.
Đây là 1 trong những đặc thù cần thiết của tam giác cân nặng và là 1 trong những phương pháp để xác lập đàng trung tuyến nhập Việc tương quan cho tới tam giác cân nặng.

Có, sở hữu tồn bên trên công thức tính chừng nhiều năm đàng trung tuyến nhập tam giác ko cân nặng ko. Công thức này được xem vì chưng căn bậc 2 của 1 phần 2 tổng bình phương nhì cạnh kề. Sau cơ, tao trừ lên đường 1 phần tư bình phương cạnh đối.

Đường trung tuyến của tam giác cân nặng không tồn tại không khí quan trọng đặc biệt nào là. Đường trung tuyến đơn giản đường thẳng liền mạch trải qua trung điểm của một cạnh và tuy nhiên song với cạnh sót lại. Nó ko tạo nên ngẫu nhiên hình dạng hay là không gian trá quan trọng đặc biệt nào là nhập tam giác cân nặng.

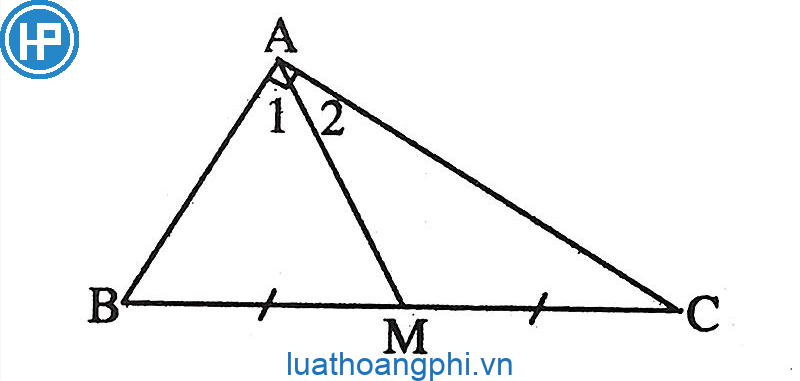
Có một quan hệ cần thiết thân mật chừng nhiều năm của đàng trung tuyến và những cạnh của tam giác cân nặng. Đường trung tuyến nhập tam giác cân nặng là đoạn trực tiếp nối trung điểm của một cạnh với đỉnh đối lập. Độ nhiều năm của đàng trung tuyến nhập tam giác cân đối 50% chừng nhiều năm cạnh đối lập.
Cho tam giác cân nặng ABC, với AB = AC, và BC là cạnh đối lập, M là trung điểm của BC. Độ nhiều năm của đàng trung tuyến AM vì chưng 50% chừng nhiều năm cạnh BC.
Ví dụ, nếu như BC = 12 centimet, thì chừng nhiều năm đàng trung tuyến AM tiếp tục là 1 trong những nửa của 12 centimet, tức là 6 centimet.
Tương tự động, đàng trung tuyến BM và đàng trung tuyến CM cũng đều có chừng nhiều năm như thế.
Vậy tao sở hữu quan hệ đơn giản: chừng nhiều năm đàng trung tuyến nhập tam giác cân đối 50% chừng nhiều năm cạnh đối lập.

Để vận dụng công thức tính chừng nhiều năm đàng trung tuyến nhập giải Việc thực tiễn, tao cần thiết thực hiện như sau:
Bước 1: Xác quyết định tam giác đã có sẵn trước vấn đề về những cạnh hoặc những bộ phận quan trọng nhằm tính chừng nhiều năm đàng trung tuyến.
Bước 2: Tính những cạnh của tam giác nếu như không được cung ứng.
Bước 3: sít dụng công thức tính chừng nhiều năm đàng trung tuyến, được xem vì chưng căn bậc 2 của 1 phần 2 tổng bình phương nhì cạnh kề. Sau cơ, trừ lên đường 1 phần tư bình phương cạnh đối. Công thức đúng chuẩn như sau:
Độ nhiều năm đàng trung tuyến = √[(2*(cạnh A)^2 + 2*(cạnh B)^2) - (cạnh C)^2]
Trong đó:
- cạnh A là cạnh kề với phần đường trung tuyến
- cạnh B là cạnh kề với phần đường trung tuyến
- cạnh C là cạnh đối lập với phần đường trung tuyến
Bước 4: Thay nhập độ quý hiếm những cạnh và đo lường và tính toán nhằm lần chừng nhiều năm đàng trung tuyến.
Bước 5: Kết luận thành phẩm và ghi ghi nhớ đơn vị chức năng thống kê giám sát cho tới chừng nhiều năm đàng trung tuyến tìm ra.
Ví dụ:
Với tam giác ABC sở hữu BA = 6cm, BC = 8cm và AC = 10cm, tao cần thiết tính chừng nhiều năm đàng trung tuyến kể từ đỉnh B cho tới đỉnh AC.
Bước 1: Tam giác ABC đang được sở hữu không thiếu vấn đề.
Bước 2: Không cần thiết đo lường và tính toán những cạnh.
Bước 3: sít dụng công thức tính chừng nhiều năm đàng trung tuyến:
Độ nhiều năm đàng trung tuyến = √[(2*(6)^2 + 2*(8)^2) - (10)^2]
= √[72 + 128 - 100]
= √[100]
= 10cm
Bước 4: Độ nhiều năm đàng trung tuyến kể từ đỉnh B cho tới đỉnh AC là 10cm.
Bước 5: Kết ngược là 10cm.

Xem thêm: bài tập về hiện tại đơn

Có, sở hữu công thức nhằm tính chừng nhiều năm đàng trung tuyến của tam giác ko cân nặng ko. Để tính chừng nhiều năm đàng trung tuyến AB của tam giác ABC ko cân nặng ko, tao dùng công thức sau đây:
AB = √(2×(AC^2 + BC^2) - AM^2)
Trong cơ, AC là chừng nhiều năm cạnh ko cân nặng của tam giác, BC là chừng nhiều năm cạnh không giống cạnh AC, và AM là chừng nhiều năm đàng cao trải qua đỉnh A của tam giác.