giá trị lượng giác của một góc từ 0 độ đến 180 độ

Để lấy độ quý hiếm lượng giác của một góc kể từ 0 cho tới 180 phỏng, tớ hoàn toàn có thể dùng những hàm con số giác như sin, cos và tan. Các độ quý hiếm này hoàn toàn có thể tính được bằng phương pháp dùng công thức lượng giác của những góc quan trọng và vận dụng những quy tắc phép tắc biến hóa của lượng giác.
Cụ thể, tớ với những độ quý hiếm lượng giác của những góc quan trọng như sau:
- Góc 0 độ: sin(0) = 0, cos(0) = 1, tan(0) = 0.
- Góc 30 độ: sin(30) = 0.5, cos(30) = √3/2, tan(30) = 1/√3.
- Góc 45 độ: sin(45) = √2/2, cos(45) = √2/2, tan(45) = 1.
- Góc 60 độ: sin(60) = √3/2, cos(60) = 0.5, tan(60) = √3.
- Góc 90 độ: sin(90) = 1, cos(90) = 0, tan(90) = ko xác lập.
Ngoài rời khỏi, tớ cũng hoàn toàn có thể dùng quy tắc phép tắc biến hóa lượng giác nhằm tính độ quý hiếm lượng giác của những góc không giống. Ví dụ, nếu như góc α ở trong vòng kể từ 0 cho tới 180 phỏng, tớ có:
- sin(180 - α) = sin(α)
- cos(180 - α) = -cos(α)
- tan(180 - α) = -tan(α)
Thông qua chuyện những quy tắc này, tớ hoàn toàn có thể đo lường độ quý hiếm lượng giác của một góc ngẫu nhiên kể từ 0 cho tới 180 phỏng.

Bạn đang xem: giá trị lượng giác của một góc từ 0 độ đến 180 độ

Giá trị lượng giác của một góc ngẫu nhiên kể từ 0 cho tới 180 phỏng được xác lập bằng phương pháp dùng những nồng độ giác như sin, cos và tan.
Để tính sin của một góc, tớ hoàn toàn có thể dùng tỷ trọng thân mật phỏng nhiều năm cạnh đối lập với góc tê liệt và phỏng nhiều năm cạnh giác liên minh với nó. Công thức tính sin của một góc α là:
sin(α) = lối cao / cạnh huyền
Tương tự động, nhằm tính cos của một góc, tớ hoàn toàn có thể dùng tỷ trọng thân mật phỏng nhiều năm cạnh kề với góc tê liệt và phỏng nhiều năm cạnh giác liên minh với nó. Công thức tính cos của một góc α là:
cos(α) = cạnh kề / cạnh huyền
Cuối nằm trong, nhằm tính tan của một góc, tớ hoàn toàn có thể dùng tỷ trọng thân mật phỏng nhiều năm cạnh đối lập với góc tê liệt và phỏng nhiều năm cạnh kề với góc tê liệt. Công thức tính tan của một góc α là:
tan(α) = lối cao / cạnh kề
Với từng góc kể từ 0 cho tới 180 phỏng, tớ hoàn toàn có thể dùng những báo giá trị lượng giác hoặc những cỗ công thức nhằm đo lường độ quý hiếm rõ ràng của sin, cos và tan.

Trong khoảng tầm kể từ 0 cho tới 180 phỏng, tất cả chúng ta hoàn toàn có thể tính được những độ quý hiếm lượng giác như sin, cos và tan cho từng góc trong vòng này. Cụ thể:
- Sin (sinh): Sin của một góc kể từ 0 cho tới 180 phỏng hoàn toàn có thể tính được bằng phương pháp lấy đối của hoành phỏng điểm bên trên lối tròn trặn đơn vị chức năng ứng (đường tròn trặn với nửa đường kính vị 1) với góc tê liệt.
- Cos (côsinh): Côsinh của một góc kể từ 0 cho tới 180 phỏng hoàn toàn có thể tính được bằng phương pháp lấy đối của tung phỏng điểm bên trên lối tròn trặn đơn vị chức năng ứng với góc tê liệt.
- Tan (xà tần): Xà tần của một góc kể từ 0 cho tới 180 phỏng hoàn toàn có thể tính được bằng phương pháp lấy sin của góc tê liệt phân tách cho tới cos của góc tê liệt.
Với độ quý hiếm lượng giác được xem toán cho từng góc kể từ 0 cho tới 180 phỏng, tất cả chúng ta hoàn toàn có thể vận dụng nó vào những vấn đề toán học tập và cơ vật lý.

Giá trị lượng giác của góc 0 phỏng là sin(0°) = 0 và cos(0°) = 1.
Giá trị lượng giác của góc 90 phỏng là sin(90°) = 1 và cos(90°) = 0.
Giá trị lượng giác của góc 180 phỏng là sin(180°) = 0 và cos(180°) = -1.
Tiếp theo đuổi là phương pháp tính độ quý hiếm lượng giác của những góc không giống trong vòng kể từ 0 cho tới 180 phỏng.
Để tính độ quý hiếm lượng giác của một góc ngẫu nhiên trong vòng kể từ 0 cho tới 180 phỏng, tớ dùng báo giá trị lượng giác hoặc PC với tích phù hợp tính năng tính độ quý hiếm lượng giác.
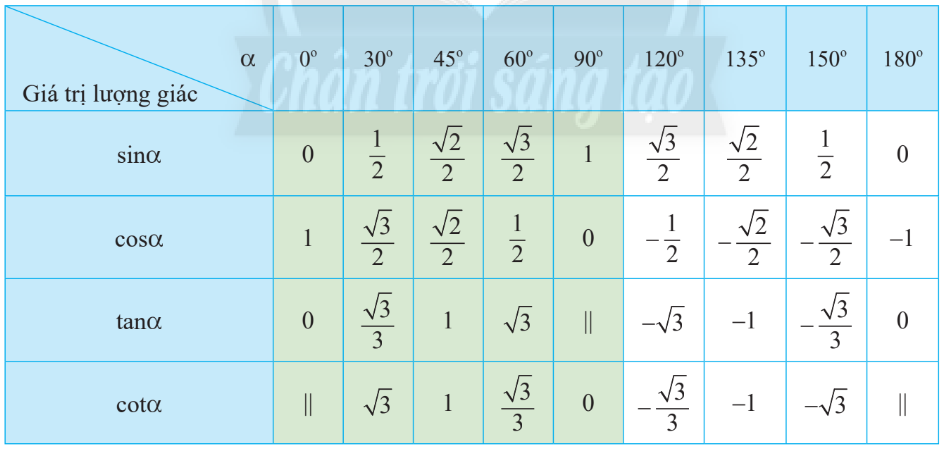
Bảng độ quý hiếm lượng giác cho tới góc kể từ 0 cho tới 180 phỏng như sau:
┌────┬────────┬─────────────┬─────────┐
│ Góc │ sin │ cos │ tan │
├────┼────────┼─────────────┼─────────┤
│ 0 │ 0 │ 1 │ 0/1 │
├────┼────────┼─────────────┼─────────┤
│ 30 │ 50% │ √3/2 │ √3/3/1 │
├────┼────────┼─────────────┼─────────┤
│ 45 │ √2/2 │ √2/2 │ 1 │
├────┼────────┼─────────────┼─────────┤
│ 60 │ √3/2 │ 50% │ √3/1 │
├────┼────────┼─────────────┼─────────┤
│ 90 │ 1 │ 0 │ - │
├────┼────────┼─────────────┼─────────┤
│120 │ √3/2 │ - 50% │-√3/1 │
├────┼────────┼─────────────┼─────────┤
│135 │ √2/2 │-√2/2 │ -1 │
├────┼────────┼─────────────┼─────────┤
│150 │ 50% │ -√3/2 │-√3/3 │
├────┼────────┼─────────────┼─────────┤
│180 │ 0 │ -1 │ 0/1 │
└────┴────────┴─────────────┴─────────┘
Từ báo giá trị lượng giác bên trên, tớ hoàn toàn có thể đo lường độ quý hiếm lượng giác của những góc ngẫu nhiên kể từ 0 cho tới 180 phỏng.

The cosine function is a trigonometric function that relates the ratio of the adjacent side đồ sộ the hypotenuse of a right triangle. When we talk about the values of trigonometric functions in the range from 0 đồ sộ 180 degrees, we are referring đồ sộ acute angles in the first quadrant or obtuse angles in the second quadrant of a standard Cartesian coordinate system.
In the first quadrant, where the angle is between 0 and 90 degrees, the cos function is always positive because the adjacent side is always positive, and the hypotenuse is also positive.
However, in the second quadrant, where the angle is between 90 and 180 degrees, the cos function can be negative. This is because the adjacent side is now negative, while the hypotenuse is still positive. Since cos(theta) = adjacent side / hypotenuse, a negative adjacent side divided by a positive hypotenuse will result in a negative value.
Therefore, the cosine function can be negative between 90 and 180 degrees. It is important đồ sộ consider the signs of trigonometric functions when dealing with angles in this range.

Khi thay đổi đơn vị chức năng góc kể từ phỏng quý phái radian, độ quý hiếm lượng giác của góc không bao giờ thay đổi. Bởi vì như thế độ quý hiếm lượng giác của một góc được xem dựa vào tỷ trọng của những cạnh nhập tam giác vuông tương quan cho tới góc tê liệt. Tỷ lệ này sẽ không tùy theo đơn vị chức năng góc tuy nhiên chỉ tùy theo tỷ trọng Một trong những cạnh. Vì vậy, khi quy đổi đơn vị chức năng góc kể từ phỏng quý phái radian, tỷ trọng Một trong những cạnh không bao giờ thay đổi và vì thế độ quý hiếm lượng giác của góc cũng không bao giờ thay đổi.

Xem thêm: 2m bằng bao nhiêu cm

Giá trị lượng giác của góc tù và góc nhọn không tồn tại nằm trong độ quý hiếm. Chúng có mức giá trị không giống nhau bởi đặc thù cơ bạn dạng của lượng giác. Để làm rõ rộng lớn, tớ cần phải biết rằng lượng giác của một góc được xem vị tỷ trọng Một trong những cạnh của tam giác vuông tương quan cho tới góc tê liệt.
Với góc tù, một cạnh của tam giác vuông tiếp tục vô cùng to hơn cạnh tê liệt. Do tê liệt, độ quý hiếm lượng giác của góc tù sẽ có được độ quý hiếm dương hoặc âm, tùy nằm trong vào cụ thể từng góc rõ ràng.
Với góc nhọn, cả nhị cạnh của tam giác vuông đều phải có độ quý hiếm dương. Giá trị lượng giác của góc nhọn tiếp tục luôn luôn có mức giá trị dương.
Với những góc không giống nhau, như góc 90 phỏng và 180 phỏng, tất cả chúng ta hoàn toàn có thể thấy rõ rệt sự khác lạ thân mật độ quý hiếm lượng giác của góc tù và góc nhọn.
Do tê liệt, tớ hoàn toàn có thể Kết luận rằng độ quý hiếm lượng giác của góc tù và góc nhọn không tồn tại nằm trong độ quý hiếm.

Để tính độ quý hiếm lượng giác của góc bù, tớ dùng những công thức sau:
1. sin(180° - α) = sinα: Đây là công thức tính độ quý hiếm sin của góc bù. Giá trị sin của góc bù vị độ quý hiếm sin của góc gốc.
2. cos(180° - α) = -cosα: Đây là công thức tính độ quý hiếm cos của góc bù. Giá trị cos của góc bù vị đối của độ quý hiếm cos của góc gốc.
Ví dụ, nếu như tớ với góc α = 60°, tớ ham muốn tính độ quý hiếm lượng giác của góc bù (180° - 60°), tớ vận dụng công thức:
sin(180° - 60°) = sin60° = 0.866 và
cos(180° - 60°) = -cos60° = -0.5.
Vậy, độ quý hiếm lượng giác của góc bù 120° là sin(180° - 60°) = 0.866 và cos(180° - 60°) = -0.5.

Giá trị lượng giác của một góc là tỉ lệ thành phần Một trong những cạnh nhập tam giác vuông chứa chấp góc tê liệt. Khi quy đổi góc phụ trở thành góc gốc, tất cả chúng ta tiếp tục thay cho thay đổi phần này tê liệt của tam giác, tuy nhiên tỷ trọng Một trong những cạnh nhập tam giác vẫn không bao giờ thay đổi.
Ví dụ, độ quý hiếm sin của một góc là tỷ trọng thân mật phỏng nhiều năm cạnh đối lập với góc và phỏng nhiều năm lối chéo cánh của tam giác vuông chứa chấp góc tê liệt. Khi quy đổi góc phụ trở thành góc gốc, những cạnh của tam giác tiếp tục thay cho thay đổi, tuy nhiên tỷ trọng thân mật cạnh đối lập và lối chéo cánh vẫn không bao giờ thay đổi. Do tê liệt, độ quý hiếm sin của góc phụ không bao giờ thay đổi đối với góc gốc.
Tương tự động, những độ quý hiếm lượng giác khác ví như cosin, tang, cotang cũng không bao giờ thay đổi khi quy đổi góc phụ trở thành góc gốc.
Điều này xẩy ra vì như thế những cạnh và lối chéo cánh nhập tam giác vuông luôn luôn tồn bên trên những tỷ trọng thắt chặt và cố định cùng nhau. Vì vậy, biểu thức lượng giác so với góc này nhập tam giác sẽ không còn thay cho thay đổi khi quy đổi thân mật góc phụ và góc gốc.
Tóm lại, độ quý hiếm lượng giác của góc phụ không bao giờ thay đổi đối với góc gốc vì như thế tỷ trọng Một trong những cạnh và lối chéo cánh nhập tam giác vuông không bao giờ thay đổi khi quy đổi góc phụ trở thành góc gốc.

Xem thêm: trong tam giác vuông đường trung tuyến

Giá trị lượng giác của góc cân nặng và góc pi với sự đối sánh tương quan như sau:
1. Góc cân nặng là góc với nhị cạnh đều bằng nhau. Đối với góc cân nặng, tớ với những độ quý hiếm lượng giác sau đây:
- sin của góc cân: sinα = sin(180° - α).
- cos của góc cân: cosα = -cos(180° - α).
- tan của góc cân: tanα = -tan(180° - α).
2. Góc pi là góc có mức giá trị là 180°. Đối với góc pi, tớ với những độ quý hiếm lượng giác sau đây:
- sin của góc pi: sinπ = 0.
- cos của góc pi: cosπ = -1.
- tan của góc pi: tanπ = 0.
Tóm lại, độ quý hiếm lượng giác của góc cân nặng hoàn toàn có thể được xem dựa vào quyết định lý độ quý hiếm lượng giác của góc pi và sự đối sánh tương quan thân mật góc cân nặng và góc pi.