nguyên hàm 1/căn x

Nguyên hàm căn x là gì?

Theo khái niệm của vẹn toàn hàm: Cho hàm số f(x) xác lập bên trên K. Hàm số F(x) được gọi là vẹn toàn hàm của hàm số f(x) bên trên K nếu như F'(x) = f(x) với từng x ∈ K.

Bạn đang xem: nguyên hàm 1/căn x

Đối với vẹn toàn hàm căn x này phần biểu thức được xem là những độ quý hiếm căn x, nhưng mà quý khách tiếp tục nên giải bọn chúng nhằm tìm ra độ quý hiếm x. 

Tìm hiểu thêm: Nguyên hàm là gì? Bảng những công thức vẹn toàn hàm vừa đủ và cụ thể nhất

Công thức vẹn toàn hàm của căn x chi tiết

Trong những dạng toán vẹn toàn hàm, vẹn toàn hàm của căn thức là một trong những dạng toán khó khăn giải quán quân. Nên bên dưới đấy là một vài công thức thông thường gặp gỡ kể từ cơ phiên bản cho tới nâng lên nhưng mà học viên sẽ tiến hành gặp gỡ.

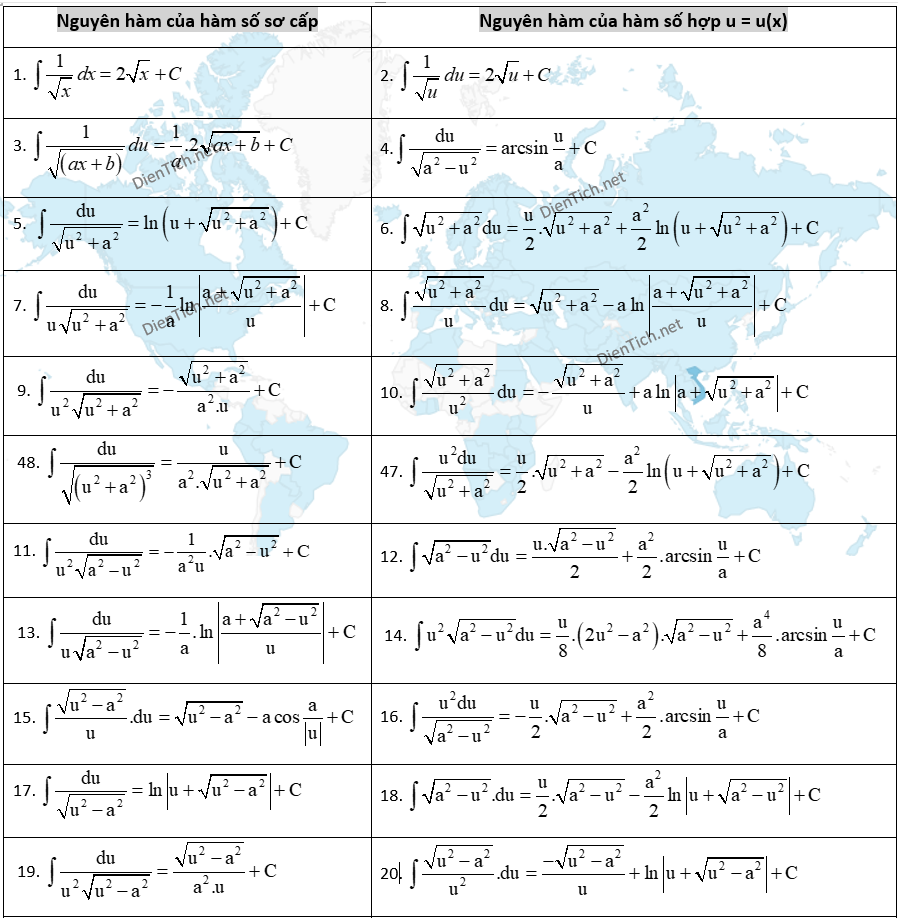
Các dạng bài xích luyện về vẹn toàn hàm căn x thông thường gặp gỡ và cơ hội giải

Trong toán căn x vẹn toàn hàm sẽ sở hữu được một vài dạng toán cơ phiên bản, tất nhiên ví dụ minh họa cụ thể sau đây:

Tìm vẹn toàn hàm của hàm chứa chấp căn thức vì chưng cách thức thay đổi đổi mới số

Cách thăm dò vẹn toàn hàm, tích phân vì chưng cách thức thay đổi biến

Cho hàm số u = u(x) sở hữu đạo hàm liên tiếp bên trên K và hàm số nó = f(u) liên tiếp sao cho tới f[u(x)] xác lập bên trên K. Khi ê nếu như F là một trong những vẹn toàn hàm của f thì:

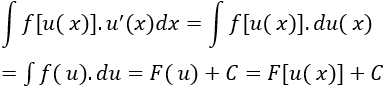
Ví dụ minh họa: 

Nguyên hàm của hàm số  là:

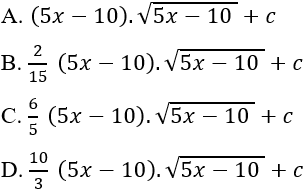
Lời giải

Ta có:

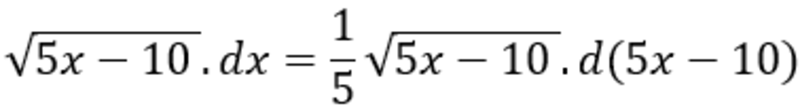
Đặt u = 5x – 10 tao được:

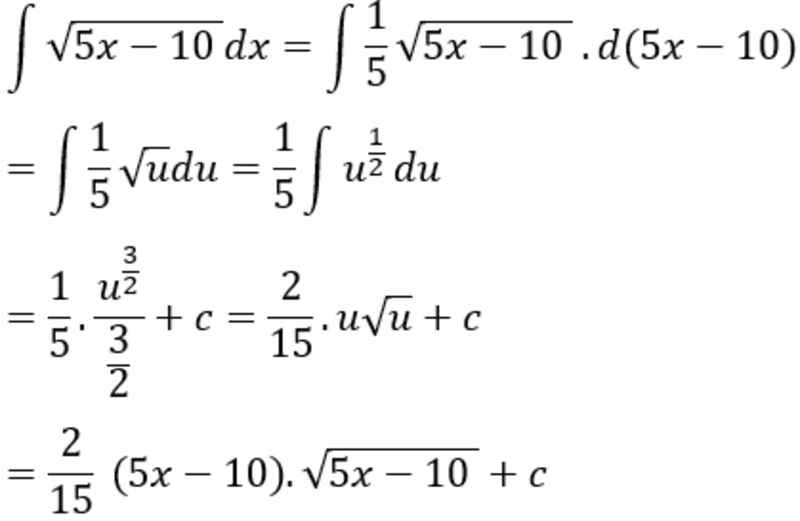
Chọn B.

Tìm vẹn toàn hàm những hàm số chứa chấp căn thức (hàm số vô tỉ) dựa vào tam thức bậc hai

Trên hạ tầng fake tam thức bậc nhị về dạng chủ yếu tắc và người sử dụng những công thức sau:

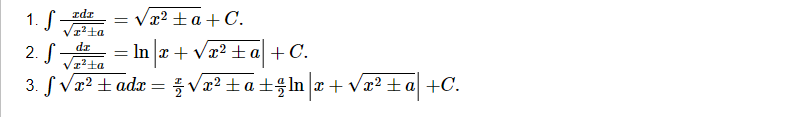
Ví dụ 1: Tìm vẹn toàn hàm những hàm số chứa chấp căn x sau: 

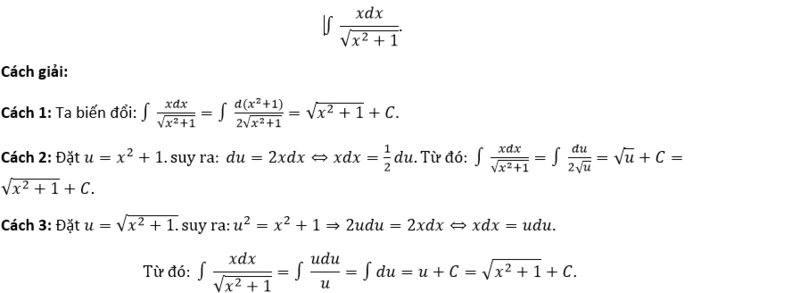
Tìm vẹn toàn hàm của hàm số $f\left(x\right)=\sqrt{\frac{x - a}{x + a}}$, với a > 0

Ta hoàn toàn có thể lựa lựa chọn 1 trong các nhị cơ hội sau:

Các vẹn toàn hàm I1 và I2 tất cả chúng ta đã biết phương pháp giải.

Tìm vẹn toàn hàm của hàm số $f\left(x\right)=\frac{dx}{\sqrt{ax + b } +\sqrt{ax + c}}$

Khử tính vô tỉ ở khuôn số bằng phương pháp trục căn thức, tao được:

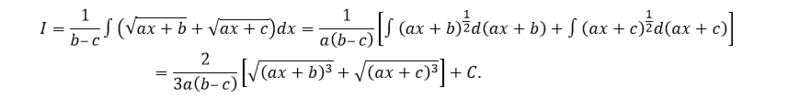
Ví dụ: Tìm vẹn toàn hàm của hàm số: $f\left(x\right)=\tan x+\frac{1}{\sqrt{2x+1}+\sqrt{2x-1}}$

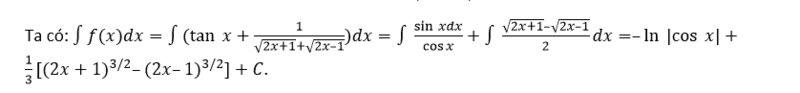
Tìm vẹn toàn hàm của hàm số chứa chấp căn thức (hàm số vô tỉ) bằng phương pháp dùng những tương đồng thức.

Ví dụ: Tìm vẹn toàn hàm của hàm số: $f\left(x\right)=\frac{x}{\sqrt[10]{x+1}}$

Xem thêm: if parents bring up a child

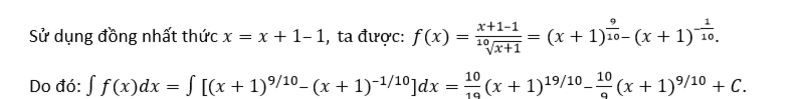
Tìm vẹn toàn hàm của hàm số: $f\left(x\right)=\frac{v\left(x\right)dx}{\sqrt{u^2}\left(x\right) \pm a}$

Ta triển khai bám theo công việc sau:

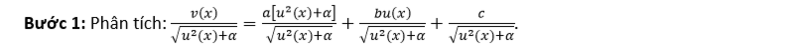
Sử dụng cách thức hằng số biến động tao xác lập được a, b, c

Bước 2: kề dụng những công thức:

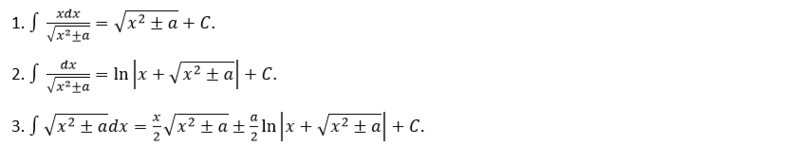
Ví dụ: Tìm vẹn toàn hàm của hàm số $f\left(x\right)=\frac{2x^2+1}{\sqrt{x^2+2x}}$

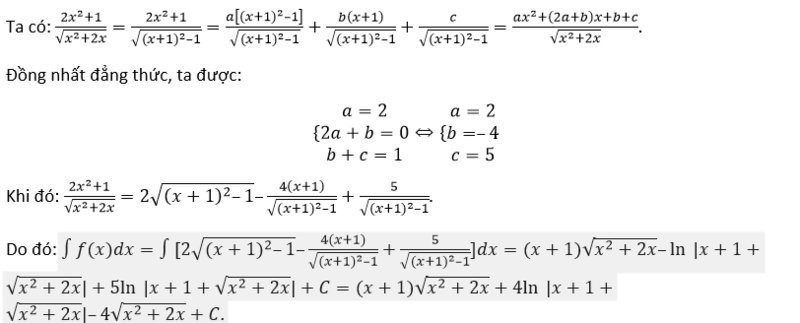
Tìm vẹn toàn hàm của hàm số: $I=\int R(x,\sqrt{a^2+x^2}).dx$

Ta triển khai bám theo công việc sau:

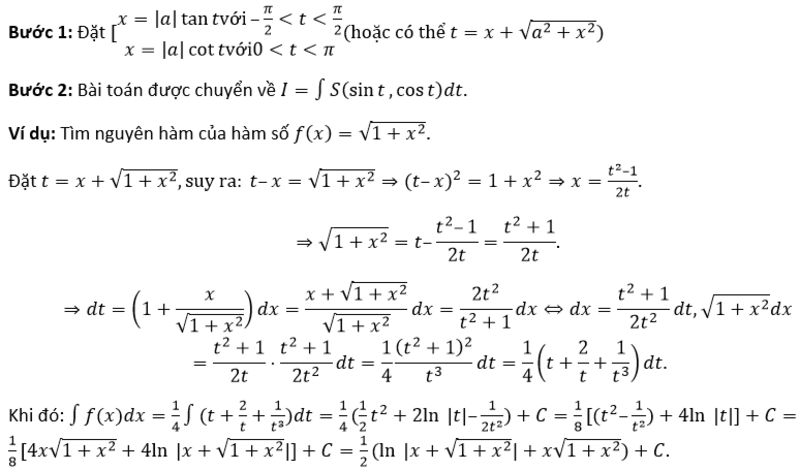
Tìm vẹn toàn hàm của hàm số: $I=\int R(x,\sqrt{x^2-a^2}).dx$

Ta triển khai bám theo công việc sau:

Một số dạng bài xích luyện vẹn toàn hàm căn x tự động luyện

Để gom học viên tiếp thu kiến thức và rèn luyện dạng toán vẹn toàn hàm của căn x cụ thể rộng lớn, bên dưới đấy là một vài dạng bài xích luyện nhưng mà quý khách hoàn toàn có thể tìm hiểu thêm và thực hành:

Bài luyện 1: Tính vẹn toàn hàm của hàm số sau

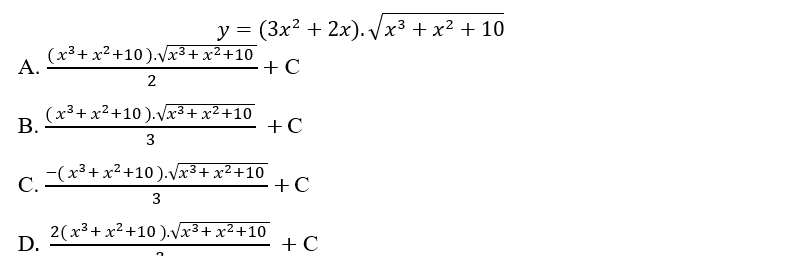
Lời giải:

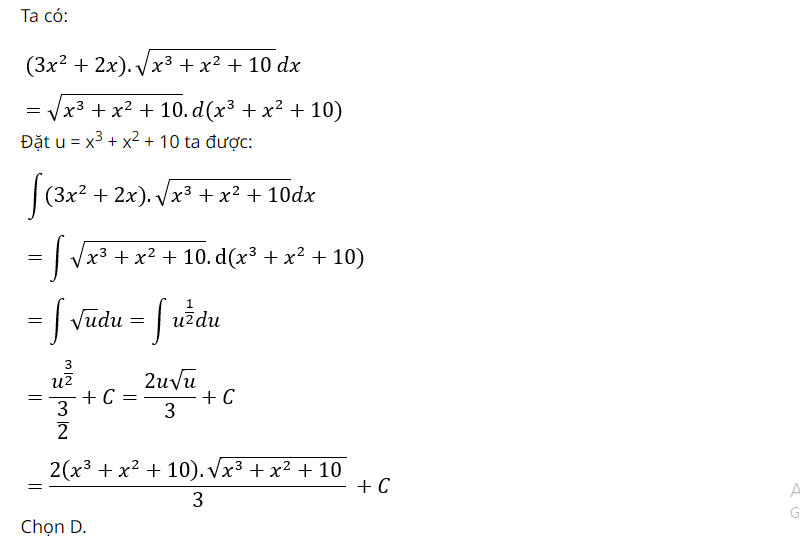
Bài luyện 2: Tính vẹn toàn hàm sau

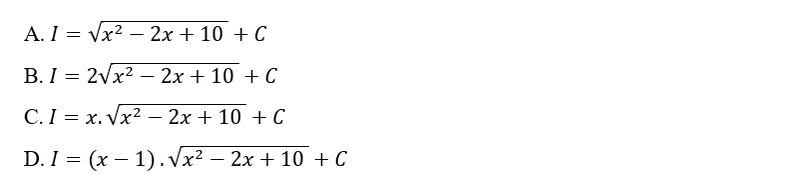
Lời giải:

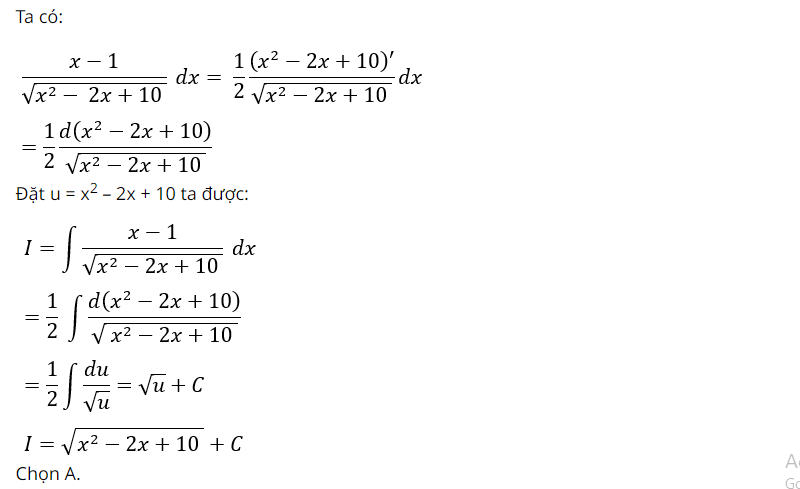
Bài luyện 3: Tính

Lời giải

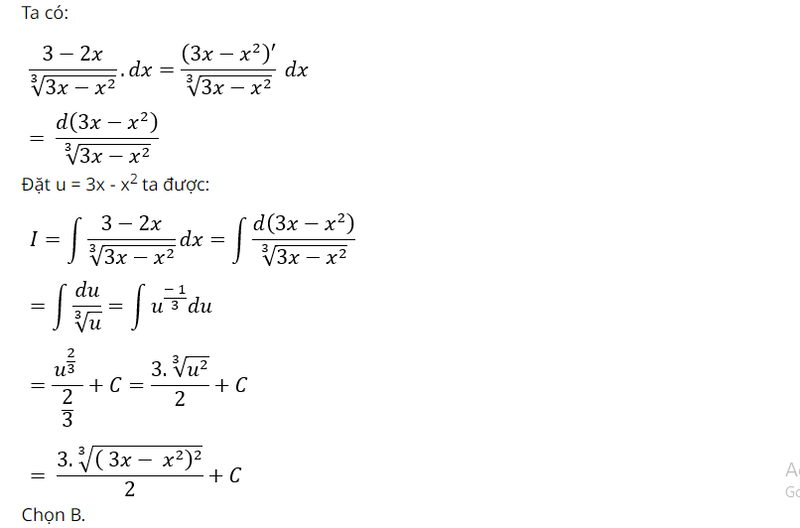
Bài luyện 4: Tính vẹn toàn hàm căn x của hàm số

Lời giải:

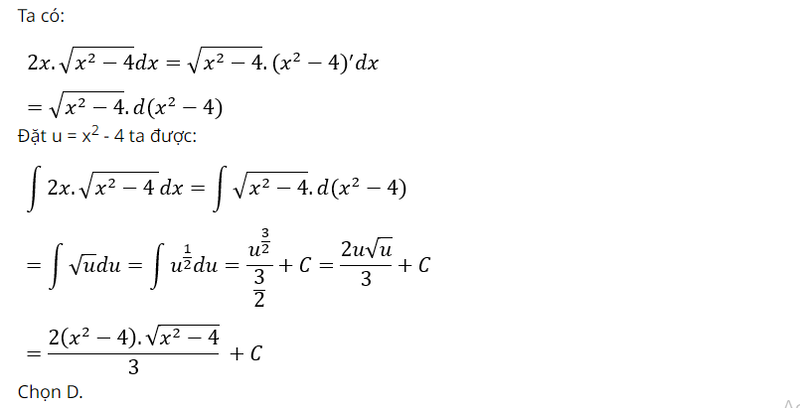
Bài luyện 5 Tính

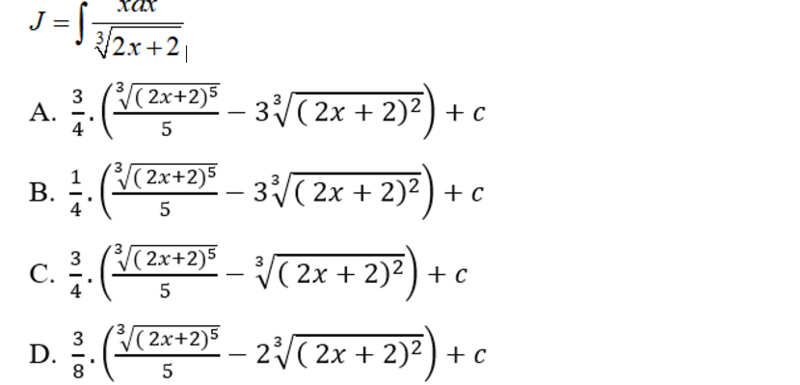
Xem thêm: đề thi cấp 3 năm 2022

Lời giải

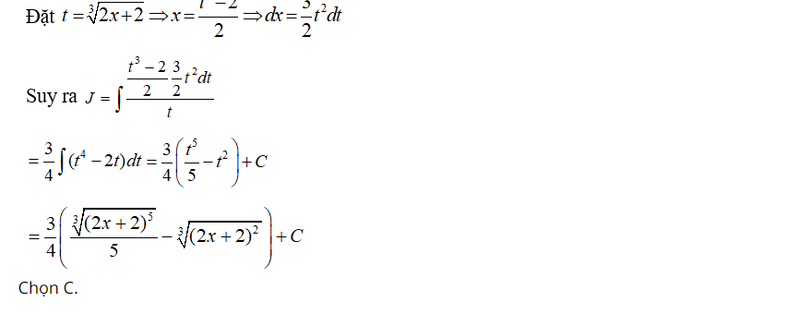
Kết luận

Trên đấy là tổ hợp vấn đề về dạng toán nguyên hàm căn x. Đây là một trong những dạng toán vẹn toàn hàm khá khó khăn, nên lúc học thì quý khách cần thiết nắm vững công thức, những dạng toán và cơ hội giải nhằm hoàn toàn có thể hoàn thiện bài xích luyện một cơ hội đúng đắn nhất nhé.