Dao động điều tiết là xê dịch nhập cơ lí chừng của vật là 1 hàm côsin (hay sin)...
Tổng thích hợp đề đua thân mật kì 2 lớp 12 toàn bộ những môn
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD
Bạn đang xem: dao động điều hòa là
DAO ĐỘNG ĐIỀU HÒA
I. Lí thuyết về xê dịch điều hòa
Quảng cáo
1. DAO ĐỘNG CƠ
- Dao động cơ: Là vận động hỗ tương xung quanh một địa điểm quan trọng đặc biệt gọi là địa điểm thăng bằng.
- Dao động tuần hoàn: Là xê dịch nhưng mà hiện trạng của vật được tái diễn như cũ, theo phía cũ sau những khoảng chừng thời hạn đều nhau xác lập.
Dao động điều hòa: Là xê dịch nhập cơ li chừng của vật là 1 hàm cosin (hay sin) của thời gian.
2.PHƯƠNG TRÌNH DAO ĐỘNG ĐIỀU HÒA
\[x = Ac{\text{os(}}\omega {\text{t + }}\varphi {\text{)}}\]
Trong đó:
+ x: li chừng của dao động
+ A: biên chừng dao động
+ ω: tần số góc của xê dịch (đơn vị: rad/s)
+ ωt+φ: trộn của xê dịch bên trên thời khắc t (đơn vị: rad)
+ φ: trộn ban sơ của dao động
3. CÁC ĐẠI LƯỢNG TRONG DAO ĐỘNG ĐIỀU HÒA
- Chu kì T: Là khoảng chừng thời hạn nhằm vật triển khai được một xê dịch toàn phần.
Đơn vị của chu kì : s (giây)
- Tần số f: Là số xê dịch toàn phần triển khai được nhập một giây.
Đơn vị của tần số: Hz (héc)
- Tần số góc ω: Là đại lượng tương tác với chu kì T hoặc với tần số f vì như thế hệ thức: $\omega = \dfrac{{2\pi }}{T} = 2\pi f$
Đơn vị của tần số góc: rad/s
- Một chu kì xê dịch vật lên đường được quãng lối là S = 4A
- Chiều nhiều năm quy trình vận động của vật là L = 2A
- Vận tốc:
$v = x' = - \omega A\sin (\omega t + \varphi ) = \omega Acos(\omega t + \varphi + \dfrac{\pi }{2})$
+ Tại VTCB: véc tơ vận tốc tức thời có tính rộng lớn đặc biệt đại: ${v_{{\text{max}}}} = \omega A$.
+ Tại biên: véc tơ vận tốc tức thời tốc vì như thế 0
+ Vận tốc thời gian nhanh trộn rộng lớn li chừng một góc $\dfrac{\pi }{2}$ và véc tơ vận tốc tức thời thay đổi chiều bên trên biên chừng.
- Gia tốc:
$a = v' = - {\omega ^2}A\cos (\omega t + \varphi ) = - {\omega ^2}x = {\omega ^2}A\cos (\omega t + \varphi + \pi )$
+ Véc tơ tốc độ luôn luôn trực tiếp thiên về địa điểm cân nặng bằng
+ Có kích cỡ tỉ trọng với kích cỡ của li độ: $\left| a \right| \sim \left| x \right|$
+ Tại biên: tốc độ có tính rộng lớn cực lớn ${a_{{\text{max}}}} = {\omega ^2}A$ , bên trên VTCB tốc độ vì như thế 0
+ Gia tốc thời gian nhanh trộn rộng lớn véc tơ vận tốc tức thời một góc $\dfrac{\pi }{2}$ và ngược trộn đối với li chừng.
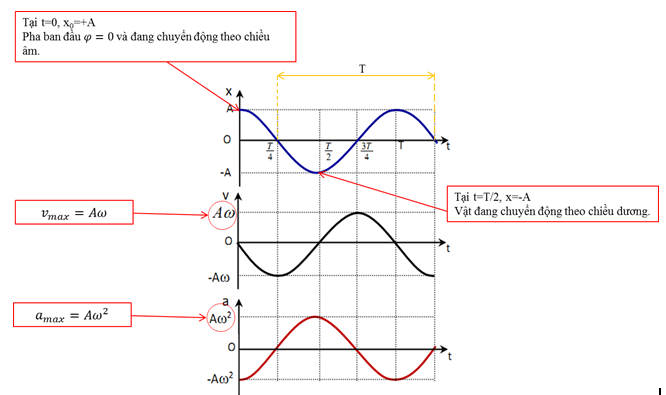
* Mô phỏng đồ dùng thị li chừng, véc tơ vận tốc tức thời, tốc độ của xê dịch điều hòa
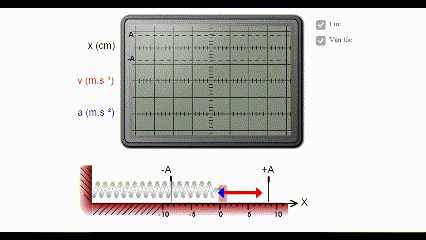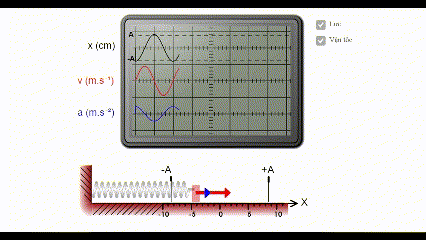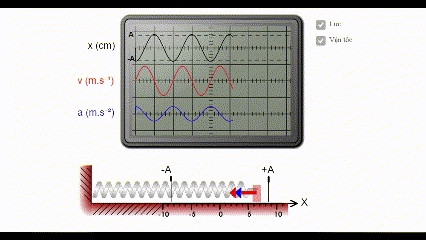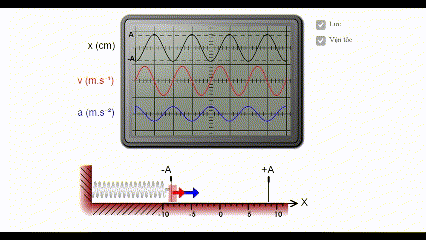
Ghi chú:
Xem thêm: viết đoạn văn từ 7 đến 10 câu
+ Công thức ông tơ tương tác thân mật x, A, v hoặc A, a, v song lập với thời gian:
\(\begin{array}{l}x = A\cos (\omega t + \varphi ) \to \cos (\omega t + \varphi ) = \dfrac{x}{A}{\rm{ }}(1)\\v = x' = - \omega A\sin (\omega t + \varphi ) \to \sin (\omega t + \varphi ) = - \dfrac{v}{{A\omega }}{\rm{ }}(2)\\a = v' = - {\omega ^2}A\cos (\omega t + \varphi ) \to \cos (\omega t + \varphi ) = - \dfrac{a}{{{\omega ^2}A}}{\rm{ }}(3)\end{array}\)
Từ (1) và (2):
$ \to {\cos ^2}(\omega t + \varphi ) + {\sin ^2}(\omega t + \varphi ) = {(\dfrac{x}{A})^2} + {( - \dfrac{v}{{A\omega }})^2} = 1$
\({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)
Từ (2) và (3):
$ \to {\cos ^2}(\omega t + \varphi ) + {\sin ^2}(\omega t + \varphi ) = {(\dfrac{a}{{A{\omega ^2}}})^2} + {( - \dfrac{v}{{A\omega }})^2} = 1$
\({A^2} = {\dfrac{a}{{{\omega ^4}}}^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)
![]()
Những công thức suy đi ra kể từ những độ quý hiếm đặc biệt đại:
$\left\{ \begin{gathered}{v_{{\text{max}}}} = A\omega \hfill \\{a_{{\text{max}}}} = A{\omega ^2} \hfill \\\end{gathered} \right. \to \omega = \dfrac{{{a_{{\text{max}}}}}}{{{v_{{\text{max}}}}}},A = \dfrac{{{v_{{\text{max}}}}^2}}{{{a_{{\text{max}}}}}}$
$\overline v = \dfrac{s}{t} = \dfrac{{4A}}{T} = \dfrac{{4A\omega }}{{2\pi }} = \dfrac{{2{v_{{\text{max}}}}}}{\pi }$ (trong cơ $\overline v $ là vận tốc tầm nhập một chu kì)
4. MỐI LIÊN HỆ GIỮA DAO ĐỘNG ĐIỀU HÒA VÀ CHUYỂN ĐỘNG TRÒN ĐỀU
DĐĐH sẽ là hình chiếu của một hóa học điểm vận động tròn xoe đều lên một trục ở trong mặt mũi bằng phẳng quy trình. Với: $A = R;\omega = \dfrac{v}{R}$.
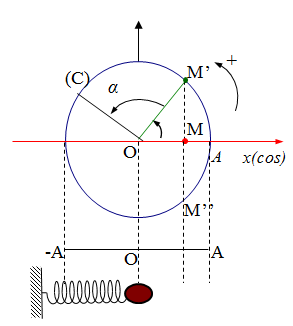
- Bước 1: Vẽ lối tròn xoe (O, R = A);
- Bước 2: t = 0: coi vật đang được ở đâu và chính thức vận động theo hướng âm hoặc dương
+ Nếu $\varphi > 0$: vật vận động theo hướng âm (về biên âm)
+ Nếu $\varphi < 0$: vật vận động theo hướng dương (về biên dương)
- Bước 3: Xác ấn định điểm cho tới nhằm xác lập góc quét dọn $\alpha $: $\Delta t = \dfrac{{\alpha .T}}{{{{360}^0}}} \Rightarrow \alpha = \dfrac{{\Delta t{{.360}^0}}}{T}$
![]()
Phương pháp tổng quát lác nhất nhằm tính véc tơ vận tốc tức thời, lối đi, thời hạn, hoặc vật qua quýt địa điểm này cơ nhập quy trình xê dịch. Ta cho tới t = 0 nhằm coi vật chính thức vận động kể từ đâu và đang di chuyển theo hướng này, tiếp sau đó nhờ vào những địa điểm quan trọng đặc biệt bên trên nhằm tính.
5. ĐỒ THỊ CỦA DAO ĐỘNG ĐIỀU HÒA
Đồ thị của dao động điều hòa là một lối hình sin
- Đồ thị cho tới ngôi trường hơp φ = 0.
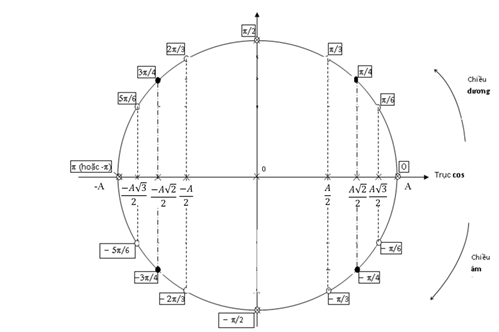
- Lược đồ dùng trộn ban sơ φ theo gót những địa điểm quan trọng đặc biệt x0:
II. Sơ đồ dùng trí tuệ lý thuyết về xê dịch điều hòa
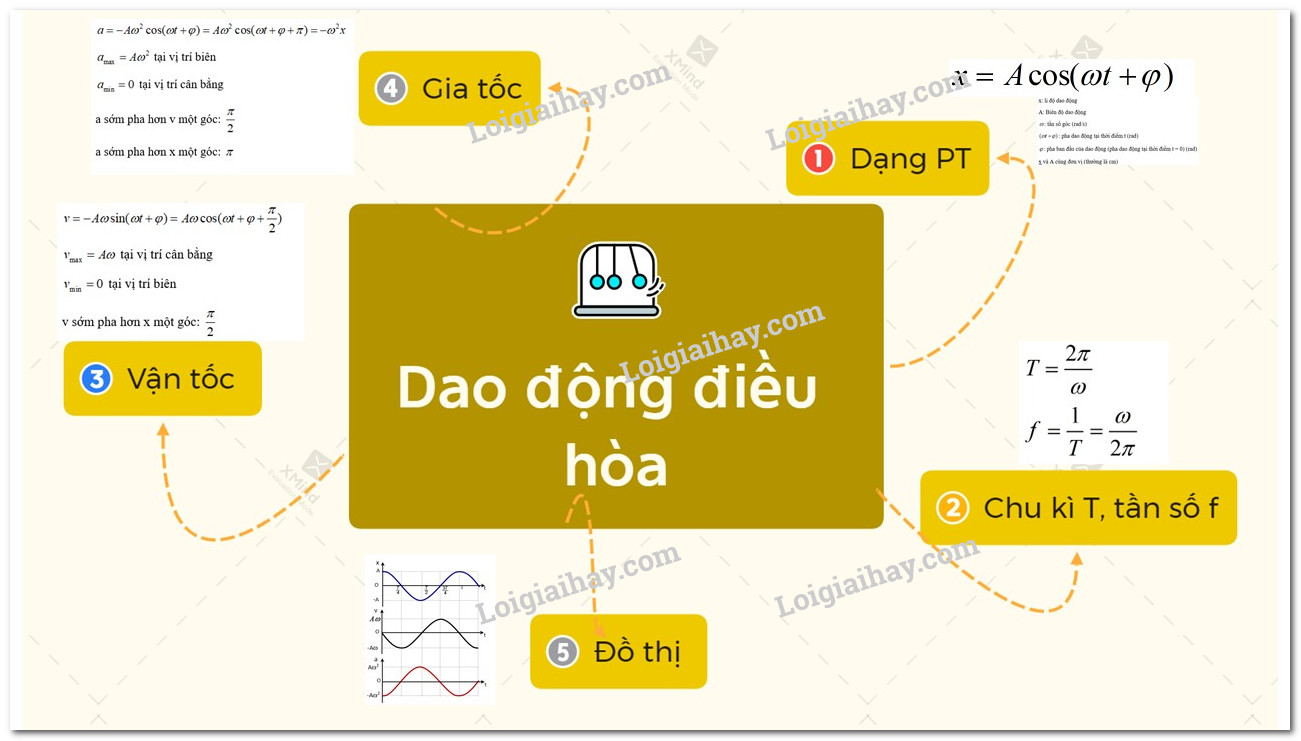
![]() Chia sẻ
Chia sẻ
-
Câu C1 trang 10 SGK Vật lý 12
Giải Câu C1 trang 10 SGK Vật lý 12
-
Bài 1 trang 8 SGK Vật lí 12
Phát biểu khái niệm của xê dịch điều hòa
-
Bài 2 trang 8 SGK Vật lí 12
Viết phương trình của xê dịch điều tiết và lý giải những đại lượng nhập phương trình.
-
Bài 3 trang 8 SGK Vật lí 12
Giải bài xích 3 trang 8 SGK Vật lí 12. Mối tương tác thân mật xê dịch điều tiết và vận động tròn xoe thể hiện nay ở phần nào?
-
Bài 4 trang 8 SGK Vật lí 12
Giải bài xích 4 trang 8 SGK Vật lí 12. Nêu khái niệm chu kì và tần số của xê dịch điều tiết.
>> Xem thêm
Xem thêm: vẽ 3 hình chiếu vuông góc của vật thể
Luyện Bài Tập Trắc nghiệm Lí lớp 12 - Xem ngay
>> Luyện đua TN trung học phổ thông & ĐH năm 2024 bên trên trang trực tuyến Tuyensinh247.com. Học từng khi, từng điểm với Thầy Cô giáo xuất sắc, không thiếu những khoá: Nền tảng lớp 12; Luyện đua thường xuyên sâu; Luyện đề đầy đủ dạng; Tổng ôn tinh lọc.










Bình luận