vectơ chỉ phương và vectơ pháp tuyến

1. Vectơ chỉ phương của lối thẳng

Định nghĩa : 

Bạn đang xem: vectơ chỉ phương và vectơ pháp tuyến

vectơ \(\vec{u}\) được gọi là vectơ chỉ phương của đường thẳng liền mạch \(∆\) nếu \(\vec{u}\) ≠ \(\vec{0}\) và giá chỉ của \(\vec{u}\) song tuy vậy hoặc trùng với \(∆\)

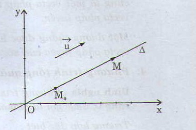
Nhận xét :

- Nếu \(\vec{u}\) là một vectơ chỉ phương của đường thẳng liền mạch \(∆\) thì \(k\vec{u} ( k≠ 0)\) cũng là 1 trong những vectơ chỉ phương của \(∆\) , bởi vậy một lối thẳng có vô số vectơ chỉ phương.

- Một đường thẳng liền mạch trọn vẹn được xác lập nếu như biết một điểm và một vectơ chỉ phương của đường thẳng liền mạch bại.

2. Phương trình thông số của lối thẳng

- Phương trình thông số của đường thẳng liền mạch \(∆\) trải qua điểm \(M_0(x_0 ;y_0)\) và nhận vectơ \(\vec{u}  = (u_1; u_2)\) thực hiện vectơ chỉ phương là :

\(∆\) : \(\left\{\begin{matrix} x= x_{0}+tu_{1}& \\ y= y_{0}+tu_{2}& \end{matrix}\right.\)

-Khi \(u_1≠ 0\) thì tỉ số \(k= \dfrac{u_{2}}{u_{1}}\) được gọi là thông số góc của đường thẳng liền mạch.

Từ trên đây, tớ đem phương trình đường thẳng liền mạch \(∆\) trải qua điểm \(M_0(x_0 ;y_0)\) và đem thông số góc k là:

\(y – y_0 = k(x – x_0)\)

Chú ý: Ta tiếp tục biết thông số góc \(k = \tan α\) với góc \(α\) là góc của đường thẳng liền mạch \(∆\) phù hợp với chiều dương của trục \(Ox\)

3. Vectơ pháp tuyến của lối thẳng 

Định nghĩa: Vectơ \(\vec{n}\) được gọi là vectơ pháp tuyến của đường thẳng liền mạch \(∆\) nếu \(\vec{n}\)  ≠ \(\vec{0}\) và \(\vec{n}\) vuông góc với vectơ chỉ phương của \(∆\)

Nhận xét:

- Nếu \(\vec{n}\)  là 1 trong những vectơ pháp tuyến của đường thẳng liền mạch \(∆\) thì k\(\vec{n}\) \((k ≠ 0)\) cũng là 1 trong những vectơ pháp tuyến của \(∆\), bởi vậy một đường thẳng liền mạch đem vô số vec tơ pháp tuyến.

- Một đường thẳng liền mạch được trọn vẹn xác lập nếu như biết một và một vectơ pháp tuyến của chính nó.

4. Phương trình tổng quát tháo của lối thẳng

Định nghĩa: Phương trình \(ax + by + c = 0\) với \(a\) và \(b\) ko đôi khi vì như thế \(0\), được gọi là phương trình tổng quát tháo của đường thẳng liền mạch.

Trường thích hợp quánh biết:

+  Nếu \(a = 0 => nó = \dfrac{-c}{b};  ∆ // Ox\) hoặc trùng Ox (khi c=0)

+ Nếu \(b = 0 => x = \dfrac{-c}{a}; ∆ // Oy\) hoặc trùng Oy (khi c=0)

+ Nếu \(c = 0 => ax + by = 0 =>  ∆\) trải qua gốc tọa độ

+ Nếu \(∆\) rời \(Ox\) bên trên \(A(a; 0)\) và \(Oy\) bên trên \(B (0; b)\) thì tớ đem phương trình đoạn chắn của đường thẳng liền mạch \(∆\) :

\(\dfrac{x}{a} + \dfrac{y}{b} = 1\)

5. Vị trí kha khá của hai tuyến phố thẳng

Xét hai tuyến phố trực tiếp  ∆₁ và ∆₂ 

Xem thêm: vẽ 3 hình chiếu vuông góc của vật thể

có phương trình tổng quát tháo thứu tự là :

a₁x+b₁y + c₁ = 0 và a₂x+b₂y +c₂ = 0

Điểm \(M_0(x_0 ;y_0)\)) là vấn đề cộng đồng của  ∆₁ và ∆₂  khi và chỉ khi \((x_0 ;y_0)\) là nghiệm của hệ nhì phương trình:

(1)  \(\left\{\begin{matrix} a_{1}x+b_{1}y +c_{1} = 0& \\ a_{2}x+b_{2}y+c_{2}= 0& \end{matrix}\right.\) 

Ta đem những tình huống sau:

a) Hệ (1) mang trong mình một nghiệm: ∆₁ cắt ∆₂

b) Hệ (1) vô nghiệm: ∆₁ // ∆₂

c) Hệ (1) đem vô số nghiệm: ∆₁ \( \equiv \)∆₂

6.Góc thân thuộc hai tuyến phố thẳng

Hai lối thẳng ∆₁ và ∆₂ cắt nhau tạo nên trở nên 4 góc.

Nếu ∆₁ không vuông góc với ∆₂ thì góc nhọn nhập số tứ góc này được gọi là góc thân thuộc hai tuyến phố thẳng ∆₁ và ∆₂.

Nếu ∆₁ vuông góc với  ∆₂ thì tớ thưa góc thân thuộc ∆₁ và ∆₂ bằng  90⁰.

Trường hợp  ∆₁ và ∆₂ song tuy vậy hoặc trùng nhau thì tớ quy ước góc giữa  ∆₁ và ∆₂ bằng 0⁰.

Như vậy góc thân thuộc hai tuyến phố trực tiếp luôn luôn bé thêm hơn hoặc bằng  90⁰  

Góc thân thuộc hai tuyến phố thẳng ∆₁ và ∆₂ được kí hiệu là \(\widehat{(\Delta _{1},\Delta _{2})}\)

Cho hai tuyến phố thẳng:

∆₁: a₁x+b₁y + c₁ = 0 

∆₂: a₂x+b₂y + c₂ = 0

Đặt \(\varphi\) = \(\widehat{(\Delta _{1},\Delta _{2})}\)

\(\cos  \varphi\) = \(\dfrac{|a_{1}.a_{2}+b_{1}.b_{2}|}{\sqrt{{a_{1}}^{2}+{b_{1}}^{2}}\sqrt{{a_{2}}^{2}+{b_{2}}^{2}}}\)

Chú ý:

+ \({\Delta _1} \bot {\Delta _2} \Leftrightarrow {n_1} \bot {n_2}\) \( \Leftrightarrow {a_1}.{a_2} + {b_1}.{b_2} = 0\)

+ Nếu \({\Delta _1}\) và \({\Delta _2}\) có phương trình nó = k₁ x + m₁ và nó = k₂ x + m₂ thì  

\({\Delta _1} \bot {\Delta _2} \Leftrightarrow {k_1}.{k_2} =  - 1\)

7. Công thức tính khoảng cách từ là một điểm đến chọn lựa một lối thẳng

Trong mặt mũi bằng phẳng \(Oxy\) cho tới đường thẳng liền mạch \(∆\) đem phương trình \(ax+by+c=0\) và điểm \(M_0(x_0 ;y_0)\)).

Xem thêm: kinh vu lan và báo hiếu

Khoảng cơ hội kể từ điểm \(M_0\) cho tới đường thẳng liền mạch \(∆\) kí hiệu là \(d(M_0,∆)\), được xem vì như thế công thức

\(d(M_0,∆)=\frac{|ax_{0}+by_{0}+c|}{\sqrt{a^{2}+b^{2}}}\)

Loigiaihay.com