quy tắc tính đạo hàm

By Admin 17/12/2023 0

Tổng phù hợp thuyết về Quy tắc tính đạo hàm không thiếu thốn, ngắn ngủi gọn gàng dễ dàng hiểu

1. Công thức

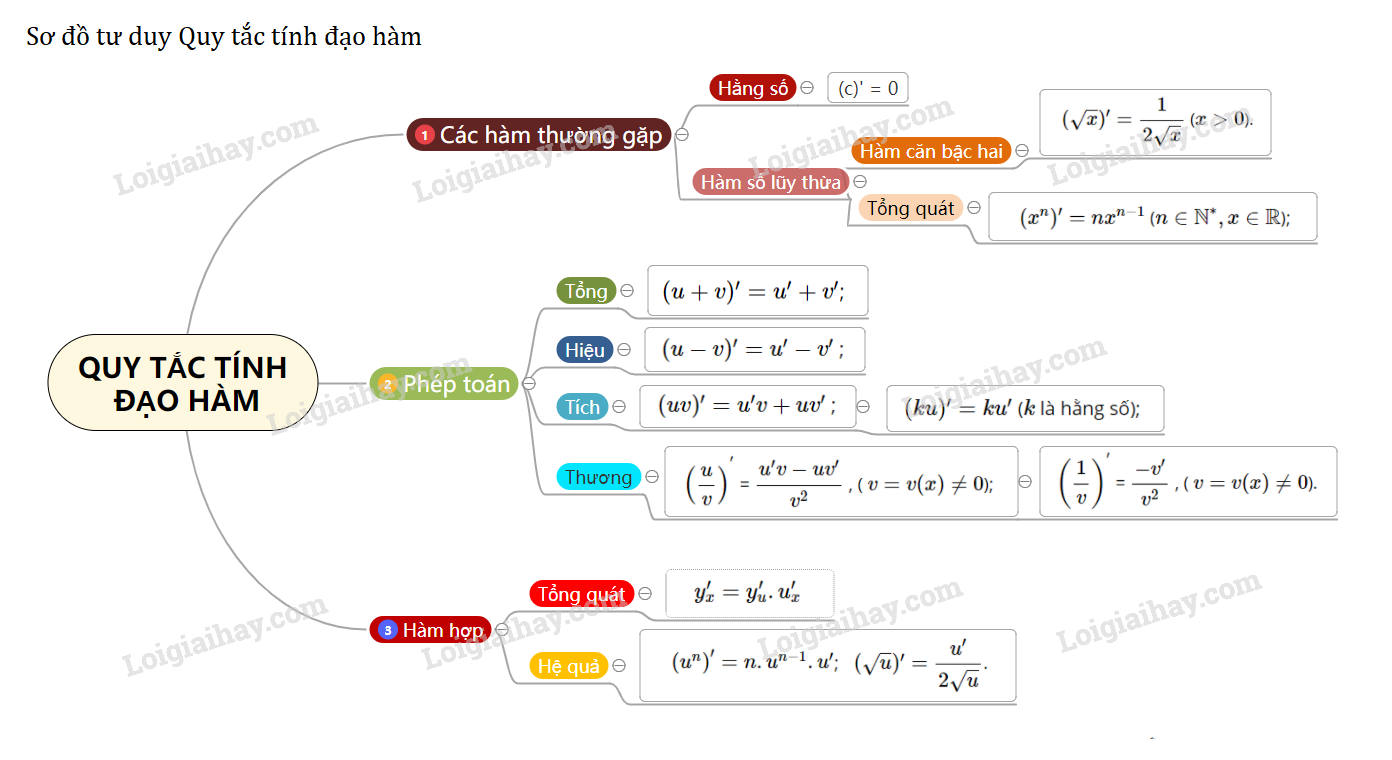
  \((c)' = 0\)       ( \(c\) là hằng số);

Bạn đang xem: quy tắc tính đạo hàm

  \((x^n)' = nx^{n-1}\) (\(n\in {\mathbb N}^*, x ∈\mathbb R\));

  \((\sqrt x)' =  \dfrac{1}{2\sqrt{x}}\) (\(x > 0\)).

2. Phép toán

\((u + v)' = u' + v' \);

\((u - v)' = u' - v'\) ;

\((uv)' = u'v + uv'\) ;

\((ku)' = ku'\) (\(k\) là hằng số);

\( \left ( \dfrac{u}{v} \right )^{^{'}}\) = \( \dfrac{u'v - uv'}{v^{2}}\) , ( \(v = v(x) ≠ 0\));

\( \left ( \dfrac{1}{v} \right )^{'}\) = \( \dfrac{-v'}{v^{2}}\) , ( \(v = v(x) ≠ 0\)).

3. Đạo hàm của hàm hợp

\[y_x' = y_u'.u_x'\]

Hệ quả: +)  \(\left( {{u^n}} \right)' = n.{u^{n - 1}}.u'\); 

Xem thêm: if parents bring up a child

             +) \((\sqrt u)' =  \dfrac{u'}{2\sqrt{u}}\).


Bình luận

Chia sẻ

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Xem thêm: trong tam giác vuông đường trung tuyến

Báo lỗi - Góp ý

2k7 Tham gia ngay lập tức group share, trao thay đổi tư liệu học hành mễn phí

>> Học trực tuyến Lớp 11 bên trên Tuyensinh247.com. Cam kết chung học viên lớp 11 học tập chất lượng tốt, trả trả ngân sách học phí nếu như học tập ko hiệu suất cao.